Đề ôn thi giữa học kì 2 Toán Lớp 12 - Đề số 1 - Trường THPT Mỹ Lộc (Có đáp án)

 ĐỀ ÔN THI 8 TUẦN KỲ II LỚP 12
ĐỀ SỐ 1
Câu 1. Đặc điểm của đồ thị hàm số bậc 3 là: 
 A. Luôn luôn có trục đối xứngB. Nhận đường thẳng nối hai cực trị làm trục đối xứng
 C. Luôn có tâm đối xứng D. Luôn nhận điểm cực trị làm tâm đối xứng
Câu 2. Hàm số y x ln x 1 đồng biến trên: 
 A. 0; B. 0; C. x 0; x 1 D. 0;  
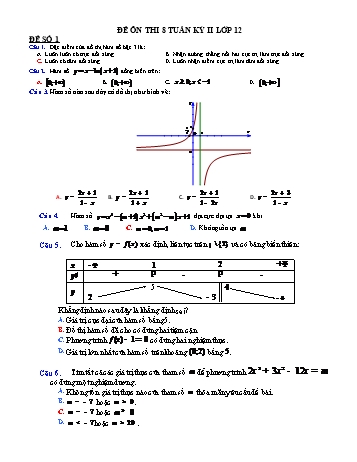
Câu 3. Hàm số nào sau đây có đồ thị như hình vẽ: 
 y
 1 1
 -
 2 O 1 x
 -2
 2x + 1 2x + 1 2x + 1 2x + 3
 A. y = B. y = C. y = D. y =
 1- x 1+ x 1- 2x 1- x
 Câu 4. Hàm số y x4 m 1 x2 m2 m x 1 đạt cực đại tại x 0 khi
 A. m 1 B. m 0 C. m 0,m 1 D. Không tồn tại m
 Câu 5. Cho hàm số y = f (x) xác định, liên tục trên ¡ \ {2} và có bảng biến thiên:
 x - ¥ 1 2 + ¥
 y¢ + P - P -
 y 5 4
 2 - 3 - ¥
 Khẳng định nào sau đây là khẳng định sai?
 A. Giá trị cực đại của hàm số bằng 5.
 B. Đồ thị hàm số đã cho có đúng hai tiệm cận.
 C. Phương trình f (x) - 1 = 0 có đúng hai nghiệm thực.
 D. Giá trị lớn nhất của hàm số trên khoảng (0;2) bằng 5.
 3 2
 Câu 6. Tìm tất cả các giá trị thực của tham số m để phương trình 2x + 3x - 12x = m 
 có đúng một nghiệm dương.
 A. Không tồn giá trị thực nào của tham số m thỏa mãn yêu cầu đề bài.
 B. m = - 7 hoặc m > 0.
 C. m = - 7 hoặc m ³ 0
 D. m 20 . Câu 7. Gọi a, A lần lượt là giá trị nhỏ nhất , giá trị lớn nhất của hàm số y x 4 x2 . Khẳng định 
 nào sau đây là sai:
 A. A2 8 B. A2 2a 4 C. 2a A 0 D. a2 A
 Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số 
 y 2sin2 x 4sin x cos x cos2 x 2 . Tính M m .
 A. 7 . B. 5 . C. 9 . D. 0 .
Câu 8. Hàm số y = ln(- x 2 + 4)+ 2e đồng biến trên tập nào?
 ù
 A. (- 2;0) B. (- 2;2) C. (- ¥ ;2) D. (- ¥ ;2ûú
 mx2 x m
Câu 9. Với giá trị m nào thì hàm số y đồng biến trên từng khoảng xác định của nó?
 x 1
 1 1 1 1
 A. 0 m B. m C. m D. m 0
 2 2 2 2
Câu 10. Cho hàm số f (x) có đạo hàm trên khoảng K và x0 K . Xét các mệnh đề sau:
 (I) Nếu hàm số đạt cực tiểu tạix0 thì f '(x0) 0 và f ''(x0) 0.
 (II) Nếu hàm số đạt cực trị tạix0 thì tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x0 song 
 song hoặc trùng với trục hoành.
 (III) Nếu hàm số đạt cực tiểu tại x0 thì với mọi x K \ { x0} , f (x) f (x0) .
 (IV) Nếu f '(x0) 0thì hàm số đạt cực trị tại x0 .
 (V) Nếu hàm số đạt cực trị tại x0 thì tồn tại a x0 và b x0 để f '(a) và f '(b) trái dấu.
 Khi đó các mệnh đề đúng là:
 A. (II),(IV), (V) B. (I), (III),(IV) C. (I),(II), (IV) D. (II), (V)
Câu 11. Xét các mệnh đề sau:
 1
 1) Đồ thị hàm số y = có hai đường tiệm cận đứng và một đường tiệm cận ngang. 
 2x - 3
 x + x 2 + x + 1
 2) Đồ thị hàm số y = có hai đường tiệm cận ngang và một đường tiệm cận đứng. 
 x
 x - 2x - 1
 3) Đồ thị hàm số y = có một đường tiệm cận ngang và hai đường tiệm cận đứng. 
 x 2 - 1
 Số mệnh đề đúng là
 A. 2. B. 3 . C. 1. D. 0 .
 x3
Câu 12. Tìm m để hàm số y m 1 x2 3 m 2 x m đồng biến trên 3; 
 3
 A. m 0 B. m 0 C. m 0 D. m 1
Câu 13. Cho hàm số y = x 3 - 3m2x 2 - m3 có đồ thị (C ). Tìm tất cả các giá trị thực của tham số m 
 để tiếp tuyến của đồ thị (C ) tại điểm có hoành độ x0 = 1 song song với đường thẳng d : y = - 3x. ém = 1
A. m = 1. B. m = - 1. C. ê . D. Không có giá trị của m .
 êm = - 1
 ëê
 16log x 3log x 2
Câu 14. Tập nghiệm của bất phương trình 3 - 3 > 0 là
 2 log x + 1
 log3 x + 3 3
 æ 1 ö æ1 ö æ 1 ö
 ç ÷ ç ÷ ç ÷
 A. ç0; ÷È ç ;1÷È ( 3;+ ¥ ) B. ç0; ÷È ( 3;+ ¥ )
 èç 3 3ø÷ èç3 ø÷ èç 3 3ø÷
 æ1 ö æ 1 ö æ1 ö
 ç ÷ ç ÷ ç ÷
 C. ç ;1÷È ( 3;+ ¥ ) D. ç0; ÷È ç ;1÷
 èç3 ø÷ èç 3 3ø÷ èç3 ø÷
 æ ö
 ç 2÷
Câu 15. Cho a và b thuộc khoảng ç0; ÷ ; a, b là những số thực tùy ý. Khẳng định nào sau đây là 
 èç eø÷
 khẳng định sai?
 a a a a b
 A. a b = (ab) B. a > a Û a > b .
 b a
 a b a+ b a b
 C. a a = a D. (a ) = (a ) .
Câu 16. Tính đạo hàm của hàm số y = e2x sin x .
 A. e2x (sin x + cosx) B. 2e2x cosx
 C. e2x (2sin x + cosx) D. e2x (2sin x - cosx)
 2
Câu 17. Đạo hàm của hàm số y log8 x 3x 8 là :
 2 2x 3
 A. y ' 2x 3 .log8 x 3x 8 B. y ' 2
 x 3x 8
 2x 3 2x 3
 C. y ' D. y ' ln8
 (x2 3x 8)ln8 x2 3x 8
 2
Câu 18. Cho phương trình log3 x - (8log3 5 + 1).log3 (9x)- 4 = 0. Khẳng định nào dưới đây 
 là khẳng định sai?
 A. 
 Phương trình đã cho có hai nghiệm x1 , x2 thỏa mãn log3 (x1x2 ) = 8log3 5 + 1.
 1
 B. x = là một nghiệm của phương trình đã cho.
 9
 C. Phương trình đã cho có đúng hai nghiệm, trong đó có một nghiệm nguyên.
 D. Phương trình đã cho có duy nhất một nghiệm.
Câu 19. Trường THPT Sơn Tây có 9 lớp chuyên và 6 lớp phổ thông ở mỗi khối. Mỗi lớp lập ra một 
 đội để tham gia cuộc thi “Hành trang tuổi 18” do Đoàn Thanh Niên trường tổ chức. Buổi ra mắt, ban 
 tổ chức chọn ra ba đội thi. Tính xác suất để ba đội thi đó nhất thiết phải có ba khối, và có cả lớp 
 chuyên và lớp phổ thông.
 21 81 883 63
 A. . B. . C. . D. .
 1892 473 946 946 Câu 20. Một đa giác đều có 35 đường chéo. Hỏi đa giác có bao nhiêu cạnh?
 A. 20 . B. 10. C. 70 . D. 35 .
 Câu 21. Trong các dãy số un dưới đây, dãy số nào là cấp số nhân?
 u1 2,u2 3
 A. . B. un 222...2.
 un 2 2un 1 un ,n 2 n ch÷ sè 2
 n * u1 10
 C. un 2 2, n ¥ . D. .
 un 4un 1,n 2
 2
 Câu 22. TXĐ của hàm số y log 1 x 3x 1 là 
 2
 3 5 3 5 3 5 3 5 
 A. D 3; ;0 B. 
  D ; 
 2 2 2 2 
 3 5 3 5 
 C.D  3;0 D. D ; 
 2 2 
 2
 Câu 23. Giải phương trình : 2log3 x 2 log3 x 4 0 .Một học sinh làm như sau :
 x 2
 Bước 1. Điều kiện : (*) .
 x 4
 Bước 2. Phương trình đã cho tương đương với 2log3 x 2 2log3 x 4 0
 2 x 3 2
 Bước 3. Hay là log3 x 2 x 4 2 x 2 x 4 1 x 6x 7 0 
 x 3 2
 Đối chiếu với điều kiện (*), suy ra phương trình đã cho có nghiệm là x 3 2 .
 Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
 A. Đúng B. Bước 3 C. Bước 1D. Bước 2
 Câu 24. Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là 5m, có bán kính 
 đáy 1m. Người ta đã rút dầu trong bồn tương ứng với 0,5m của đường kính đáy. Tính thể tích gần 
 đúng nhất của khối dầu còn lại trong bồn ( theo đơn vị m3 )
 A. 11,781 m3 B. 12,637 m3 C. 14,923m3 D. 8,307 m3
 Câu 25. Cặp hàm số nào sau đây có tính chất: Có một hàm số là nguyên hàm của hàm số còn lại?
 2 2 1 2 x - x
A. sin2x và cos x B. tan x và C. sin2x và sin x D.e và e
 cos2 x2
 Câu 26. Hình 12 mặt đều có các mặt là :
 A. Ngũ giác đều B. Tứ giác đều C. Tam giác đều D. Lục giác đều
 Câu 27. Cho lăng trụ tam giác đều có diện tích mặt bên và mặt đáy lần lượt là 2cm2 và 3cm2 . Xác 
 định thể tích lăng trụ trên.
 3
 A. 6 B. 3 C. 3 3 D. 
 3
 Câu 28. Cho hình chópS.ABC đáy ABC là tam giác vuông tại B,AB = a;BC = a 3 có hai mặt phẳng 
 (SAB);(SAC) cùng vuông góc với đáy. Góc giữa SC với mặt đáy bằng 600 . Tính khoảng cách từ A đến 
 mặt (SBC). 4a 39 a 39 2a 39 2a 39
 A. B. C. D. 
 13 13 39 13
 Câu 29. Tứ diện SABC, có SA, SB, SC đôi một vuông góc, SA=SB=2a, SC=4a, thể tích khối cầu 
 ngoại tiếp tứ diện SABC là: A. 32 a3 6 B. 24 a3 6 C. 16 a3 6 D. 8 a3 6
 Câu 30. Cho lăng trụ tam giácABC.A 'B 'C ' . Gọi M ,N,P lần lượt là trung điểm của các cạnh 
 A 'B ',BC,CC '. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chứa điểm B có thể tích 
 V
 là V . Gọi V là thể tích khối lăng trụ. Tính tỉ số 1 .
 1 V
 61 37 25 49
 A. B. C. D. 
 144 144 144 144
 Câu 31. Khai triển mặt xung quanh của một hình nón ta được hình quạt tròn có bán kính bằng 10cm, 
 độ dài cung tròn là 12 cm.Thì chiều cao của khối nón là:
 8 3
 A. 8 3 cm B. 8 2 cm C. cm D. 8cm
 3
 ' ' ' ' ' '
Câu 31: Cho lăng trụ ABCD.A'B CD .Gọi V là thể tích khối lăng trụ ABCD.A'B CD ,V1 là thể tích khối 
 V
chóp A'.ABCD thì bằng: A. 3 B. 2 C. 1 D. 4
 V1
 Câu 32. Cho hình chóp S . ABCD có đáy ABCD là vuông cạnh 2a, mặt bên SAB là tam 
 giác cân nằm trong mặt phẳng vuông góc với đáy, ·ASB 120 . Tính bán kính mặt cầu (S) ngoại 
 tiếp hình chóp.
 2a 21 a
 A. B. a C. D. Kết quả khác
 2 3 2
 Câu 33. Cho một hình nón (N) có đáy là hình tròn tâm O, đường kính 2a và đường cao SO = 2a. 
 Cho điểm H thay đổi trên đoạn thẳng SO. Mặt phẳng (P) vuông góc với SO tại H và cắt hình 
 nón theo đường tròn (C ). Khối nón có đỉnh là O và đáy là hình tròn (C ) có thể tích lớn nhất bằng 
 bao nhiêu?
 7pa3 8pa3 11pa3 32pa3
 A. . B. . C. . D. .
 81 81 81 81
 Câu 34. Một công ty chuyên sản xuất gỗ muốn thiết kế các thùng đựng hàng bên trong dạng hình lăng 
 trụ tứ giác đều không nắp, có thể tích là 62,5dm3 . Để tiết kiệm vật liệu làm thùng, người ta cần thiết 
 kế thùng sao cho tổng S của diện tích xung quanh và diện tích mặt đáy là nhỏ nhất, S bằng
 A. 50 5dm2 B. 106,25dm2 C. 75dm2 D. 125dm2
 Câu 35. ch Cho hình phẳng (H) như hình vẽ 
 bên. Diện tích 
 của hình (H) là:
 49 50
 A. B. 
 3 3
 7 8
 C. D. 
 3 3 Câu 36. Cho hàm số y f x có đồ thị 
 như hình vẽ. Chọn khẳng định sai.
 A. lim f x .
 x 0
 1
 B. Hàm số liên tục tại x .
 3
 C. lim f x lim f x .
 x x 
 D. lim f x .
 x 1 
 Câu 37. Tìm nguyên hàm của hàm số f (x) cos xsin 3x
 1 1
 A. f (x)dx cos 4x cos 2x C . B. f (x)dx cos 4x cos 2x C .
 8 4 
 1 1 1 1
 C. f (x)dx cos 4x cos 2x C . D. f (x)dx cos 4x cos 2x C .
 4 2 8 4
 x
 Câu 38. Tìm nguyên hàm của hàm số f (x) 
 2x2 1
 1
 A. f (x)dx 2x2 1 C . B. f (x)dx C .
 2
 2 2x 1
 1 1
 C. f (x)dx 2x2 1 C . D. f (x)dx 2x2 1 C .
 4 2
 Câu 39. Chọn phát biểu đúng:
 1 1 1 1 1 x
 A. dx ln sin x C . B. dx C . C. dx e x C D. dx C .
 sin x x x2 ex x 2
 Câu 40. Trong mặt phẳng tọa độ Oxy xét hai hình H1,H2 , được xác định như 
 2 2
 H1 M x, y / log 1 x y 1 log x y 
 2 2
Sau: H2 M x, y / log 2 x y 2 log x y 
 S2
Gọi S1,S2 lần lượt là diện tích của các hình H1,H2 . Tính tỉ số 
 S1
 A. 99B. 101C. 102D. 100
 x 1
 Câu 41. Cho hàm số y . Với giá trị nào của m thì đồ thị hàm số không có tiệm cận đứng?
 x2 4x m A. m 4 B. m 4 C. m 4 D. m 4
 1
 Câu 42. Gọi H là hình phẳng giới hạn bởi C : y 2 x;d : y x;x 4 . Quay H xung quanh 
 2
 80 112 16 
 trục Ox ta được khối tròn xoay có thể tích là: A. B. C. D. 32 
 3 3 3
 Câu 43. Trong không gian Oxyz. Khoảng cách giữa hai mặt phẳng ( P ) : 5x – 2y + 3z = 0 và 
 ( Q ): 5x – 2y + 3z -11= 0 là 
 11 2 12 7
 A . B. C. D. 
 38 15 7 3 3
 Câu 44. Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng tiếp xúc với mặt cầu 
 (S): x2 y2 z2 2x 4y 4z 0 tại điểm A(3; 4;3) .
 A. 4x 4 y 2z 17 0 B. 2x 2y z 17 0
 C. 2x 4y z 17 0 D. x y z 17 0
 Câu 45. Trong không gian Oxyz cho hai mặt phẳng (P): 3x 4z 5 0 và (Q): 2x 2y z 1 0 . 
 Góc giữa hai mặt phẳng trên bằng
 0
 2 0 0 0
 A. B. 0,481 C. 48 11' D. 77 37'
 3 
 Câu 46. Mặt phẳng (Q) song song với mp(P): x+2y+z-4=0 và cách D(1;0;3) một khoảng bằng 
 6 có phương trình là
 A.x+2y+z+2=0 B.x+2y-z-10=0 C.x+2y+z-10=0 D.x+2y+z+2=0 và x+2y+z-10=0
 Câu 47. Cho (S) là mặt cầu tâm I(2; 1; -1) và tiếp xúc với mặt phẳng (P) có phương trình: 2x – 
 2y – z + 3 = 0. Khi đó, bán kính của (S) là:
 4 1
 A. B.2 C. D.3
 3 3
 Câu 48. Trong mặt phẳng Oxyz. Viết phương trình mặt phẳng qua điểm M( 2 ; -3 ; 1 ) và 
 vuông góc với hai mặt phẳng ( P ) : 2x + 3y – 2z + 5 = 0 , ( Q ) : x + 5y – 5z + 14 = 0 
A. 2x + 3y – 5z - 6 = 0 B . 15x - 7y + 7z - 16 = 0
C. 10x - 16y – 14z - 7 = 0 D. 5x - 8y – 7z - 27 = 0
 Câu 49. Phú An ước mơ muốn mở công ty riêng, cần vốn ít nhất 600 triệu đồng. Ra trường, hai công 
 ty mời anh về làm. Công ty thứ nhất trả lương 7 triệu đồng/tháng và sau mỗi năm tăng 1 triệu 
 đồng/tháng. Công ty thứ hai trả lương 5 triệu đồng/tháng và sau mỗi năm tăng gấp rưỡi. Mỗi công 
 ty đều thưởng lương tháng thứ 13 mỗi năm. Phú An nên lựa chọn công ty nào để thực hiện ước mơ 
 sớm nhất và là bao nhiêu năm sau khi ra trường biết hàng tháng Phú An phải tiêu dùng hết 2 triệu 
 đồng?
 A. Công ty thứ hai sau 5 năm. B. Công ty thứ nhất sau 6 năm.
 C. Công ty thứ hai sau 6 năm. D. Công ty thứ nhất sau 5 năm. Câu 50. Cho tứ Phần không gian bên trong của chai rượu có hình dạng như hình bên. Biết bán kính 
 đáy bằng R = 4,5cm, bán kính cổ r = 1,5cm, AB = 4,5cm,BC = 6,5cm,CD = 20cm. Thể tích 
 phần không gian bên trong của chai rượu đó bằng
 3321p 7695p 957p
 A. (cm3). B. (cm3). C. (cm3). D. 478p (cm3).
 8 16 2
 A
 r
 B
 C
 D
 R