Đề ôn thi giữa học kì 2 Toán Lớp 12 - Đề số 3 - Trường THPT Mỹ Lộc

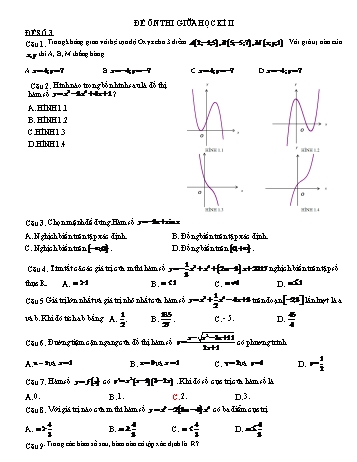
 ĐỀ ÔN THI GIỮA HỌC KÌ II
ĐỀ SỐ 3
Câu 1. Trong không gian với hệ tọa độ Oxyz cho 3 điểm A 2; 1;5 , B 5; 5;7 , M x; y;1 . Với giá trị nào của 
x, y thì A, B, M thẳng hàng.
A. x 4; y 7 B. x 4; y 7 C. x 4; y 7 D. x 4; y 7 .
 Câu 2. Hình nào trong bốn hình sau là đồ thị 
 hàm số y x3 3x2 4x 1 ?
 A. HÌNH 1.1
 B. HÌNH 1.2
 C.HÌNH 1.3
 D.HÌNH 1.4
Câu 3. Chọn mệnh đề đúng.Hàm số y 3x sin x 
A. Nghịch biến trên tập xác định. B. Đồng biến trên tập xác định.
C. Nghịch biến trên ; 0 . D. Đồng biến trên 0; .
 1
Câu 4. Tìm tất cả các giá trị của m thì hàm số y x3 x2 2m 3 x 2017 nghịch biến trên tập số 
 3
thực R. A. m 1 B. m 1 C. m 1 D. m 1
 1
Câu 5 Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y x3 x2 4x 3 trên đoạn 2;3 lần lượt là a 
 2 
 1 185 45
và b. Khi đó tích ab bằng A. . B. . C. - 5.D. 
 2 27 4
 x x2 3x 11
Câu 6. Đường tiệm cận ngang của đồ thị hàm số y có phương trình
 2x 1
 1
A. x 2và x 1 B. x 0 và x 1 C. y 2 và y 1 D. y 
 2
Câu 7. Hàm số y f x có y ' x 2 x 1 3 2x . Khi đó số cực trị của hàm số là
A. 0.B. 1.C. 2.D. 3. 
Câu 8. Với giá trị nào của m thì hàm số y x 4 2 3m 4 x 2 có ba điểm cực trị
 4 4 4 4
A. m B. m C. m D. m 
 3 3 3 3
Câu 9. Trong các hàm số sau, hàm nào có tập xác định là R? 3 2 1 5
 A. y ex x B. y x2 x 4 C. y x D. y 3 x 
 x
 1
 2 3
Câu 10. Cho f (x)dx 3 . Tính f (3x 1)dx A. 0.B. 1. C. 2.D. 9. 
 1 0
Câu 11. Phương trình x3 3x m có ba nghiệm phân biệt khi
A. m 2 hoặc m 2 . B. m 2 hoặc m 2 C. m 2 D. 2 m 2 
Câu 12: Một người nông dân có 15 000 000 đồng để 
làm một cái hàng rào hình chữ E dọc theo một con 
sông (như hình vẽ) để làm một khu đất có hai phần chữ 
nhật để trồng rau. Đối với mặt hàng rào song song với 
bờ sông thì chi phí nguyên vật liệu là 60 000 đồng một 
mét, còn đối với ba mặt hàng rào song song nhau thì 
chi phí nguyên vật liệu là 50 000 đồng một mét. Tìm 
diện tích lớn nhất của đất rào thu được 
 A. 6250m2 B. 1250m2 C. 3125m2 D. 50m2
 x 1
Câu 13: Đồ thị hàm số y không có tiệm cận ngang khi và chỉ khi :
 mx2 1
 A. m 0 B. m 0 C. m 0 D. m 0
Câu 14. Rút gọn biểu thức A a2 3 ab2 a5 b ;với a 0; b 0 ta được kết quả
 5 1 19 3 5 4 5 3
A. a 6b 4 B. a 6 b 4 C. a 4b 5 . D. a 6b 4
Câu 15. Cho a 0, b 0 , Đẳng thức nào dưới đây thỏa mãn điều kiện : a2 4b2 12ab .
 1
 A. log a logb log12 B. log(a 2b) 2log 2 log a logb 
 2
 C. log a2 logb2 log 12ab D. 2log a l2ogb log12 log ab
 ex e x
Câu 16. Cho hàm số f x 
 ex e x
 4 ex 2
 f / x f / x ex e x f / x f / x 
A. 2 B. C. 2 D. 2
 ex e x ex e x ex e x 
Câu 17. Tìm mệnh đề sai trong các mệnh đề sau
A. Hàm số y loga x có tập xác định là khoảng 0; . 
B. Hàm số y loga x với a 1 đồng biến trên khoảng 0; . 
C. Hàm số y loga x với 0 a 1 nghịch biến trên khoảng 0; .
D. Đồ thị hàm số y loga x có tiệm cận ngang là trục hoành. x x 2 x 11 25 52 29
Câu 18. Cho 5 3 . Giá trị 25 5 là: A. B. C. D. .
 3 3 3 3
Câu 19. Bất phương trình log3 3x 2 3 có nghiệm là 
 11 25 5 11
A. x B. x C. x D. x 
 3 3 3 3
Câu 20. Một người gởi tiết kiệm A đồng với lãi suất 7,56% một năm và lãi hàng năm được nhập vào 
vốn. Hỏi sau bao nhiêu năm người đó sẽ có ít nhất số tiền gấp đôi số tiền ban đầu, giả sử lãi suất không 
thay đổi.
A. 7.B. 8.C. 9.D. 10.
 2x 1 x
Câu 21. Phương trình 3 4.3 1 0 có hai nghiệm x1 , x2 thỏa
A. 2x1 x2 0 B. x1 2x2 1.C, x1 x2 2 D. x1 x2 1
Câu 22. Phương trình 32x m 1 3x m 0 có đúng hai nghiệm phân biệt khi
A. m = 1. B. m = 0. C. m 0 . D. 0 m 1
Câu 23. Một học sinh trình bày lời giải phương trình log2 x 3log x log x 0 * theo các bước 
 2 2 1 
 2
 2
 Bước 1 : * 2log2 x 2log2 x 0 , x 0
 Bước 2 : log2 x 0 hoặc log2 x 1, x 0 
 1
 Bước 3 : x 1 hoặc x 
 2
 1 
 Bước 4 : Phương trình có tập nghiệm S ;1
 2 
Trình bày lời giải phương trình trên sai trong bước nào dưới đây
A. Bước 1.B. Bước 2. C. Bước 3. D. Bước 4.
Câu24. Khi quan sát quá trình sao chép tế bào trong phòng thí nghiệm sinh học, nhà sinh vật học nhận thấy các 
tế bào tăng gấp đôi mỗi phút. Biết sau một thời gian t giờ thì có 100 000 tế bào và ban đầu có 1 tế bào duy nhất. 
Tìm t. A. t 16,61 phút B. t 16,5 phútC. t 15 phútD. t 15,5 phút
Câu 25: Tập nghiệm của bất phương trình 4x 2.25x 10x là :
 2 
A. log2 2; B. log 5 2; C. ;log2 D. 
 5
 5 2 
Câu 26: Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y f x , y g x và hai đường 
thẳng x a, x b a b là:
 b b b b
 2
 A. S f x g x dx B. S f x g x dx C. S f x g x dx D. S f x g x dx
 a a a a
 2x4 3
Câu 27: Cho hàm số f x . Chọn phương án đúng:
 x2 2x3 3 2x3 3
 A. f x dx C B. f x dx C
 3 x 3 x
 3 2x3 3
 C. f x dx 2x3 C D. f x dx C
 x 3 2x
 b
Câu 28: Cho p(x) là một đa thức của x. Cách tính p(x).sin ax.dx nào sau đây đúng:
 a 
 du p'(x)dx
 u p(x) u p(x) du p'(x)dx
A.Đặt 1 B. Đặt 
 dv sin axdx v cosax dv sin axdx v a.cosax
 a
 du p'(x)dx
 u p(x) du p'(x)dx u p(x) 
C.Đặt D. 1 Đặt
 dv sin axdx v a.cosax dv sin axdx v cosax
 a
 5
 2 x 8 15 16 15
Câu 29: Tính J 1 2sin dx là: A. J B. J C. J D. J 
 0 4 15 8 15 16
 x
Câu 30: Tìm nguyên hàm của hàm số f (x) 
 x2 2x 3
 1 3
 A. f (x)dx ln x 1 ln x 3 C . B. f (x)dx ln x 1 3ln x 3 C .
 4 4 
 1 3 1 1
 C. f (x)dx ln x 1 ln 3 x C . D. f (x)dx ln x 1 ln x 3 C .
 4 4 4 4
Câu 31: Ở hình bên, ta có parabol y x2 2x 2 , tiếp tuyến với nó tại 
điểm M 3;5 . Diện tích phần gạch chéo là:
A. 9 B. 10 C. 12 D. 15
Câu 33. Cho khối chóp S.ABCD có đáy ABCD là hình vuông, đường chéo AC a 2 , SA  ABCD . 
Cạnh bên SC tạo với đáy một góc 600 . Thể tích khối chóp S.ABCD bằng
 a3 6
A. B. a3 6 C. a2 D. a 6
 3 Câu 32: Một cái chuông có dạng như hình vẽ. Giả sử khi cắt chuông 
 bởi mặt phẳng qua trục của chuông, được thiết diện có đường viền là 
 một phần parabol ( hình vẽ ). Biết chuông cao 4m, và bán kính của 
 miệng chuông là 2 2 . Tính thể tích chuông?
 A. 6 B. 12 
 3
 C. 2 D. 16 
Câu 34. Cho hình chóp S.ABC có đáy ABC đều cạnh a, tam giác SBC cân tại S và nằm trong mặt phẳng 
 3a
vuông góc với (ABC). Khoảng cách từ điểm S đến mặt phẳng (ABC) bằng . Cạnh SA hợp với đáy 
 2
 0 0 0 0
một góc bằng A. 60 B. 30 C. 45 D. 90
 a3 3
Câu 35. Cho khối chóp đều S.ABCD có cạnh đáy bằng a, có thể tích là . Khoảng cách từ S đến 
 8
 3 3a 3a 3 3a a
 ACD là A. B. C. D. 
 4 2 8 2
Câu 36. Cho khối chóp S.ABC. Gọi A’, B’ theo thứ tự là trung điểm của các đoạn thẳng SA, SB. Trên 
 V
đoạn thẳng SC lấy C’ thỏa 3SC’ = SC. Tỉ số thể tích S.A ' B 'C ' là
 VS.ABC
 1 1 1 1
 A. . B. . C. . D. .
 4 12 6 2
Câu 37. Một phòng học có dạng là một hình hộp chữ nhật có chiều dài là 8m, chiều rộng là 6m, thể tích 
là 192m3 . Người ta muốn quét vôi trần nhà và bốn bức tường phía trong phòng. Biết diện tích các cửa 
bằng 10m 2 . Hãy tính diện tích cần quét vôi. 
 2 2 2 2
A. 182m . B. 134m .. C. 144m . D. 96m .
Câu 38. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại B với BA = BC = a, biết A’B 
hợp với đáy ABC một góc 600 . Thể tích khối lăng trụ bằng
 a3 3 a3 3 1 a3 3
A. B. C. a2 D. 
 9 2 2 6
Câu 39. Cho khối chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, góc SAC bằng 450 . Diện tích 
xung quanh của hình nón ngoại tiếp hình chóp S.ABCD bằng
 a2 2 a2 2
A. a2 2 B. a2 2 C. D. 
 2 3
Câu 40. Cho một hình cầu S . Mặt phẳng P cắt hình cầu theo một hình tròn có chu vi 2,4 a . 
Khoảng cách từ tâm mặt cầu đến P bằng 1,6a. Diện tích mặt cầu và thể tích của khối cầu lần lượt là
 32 8 32 a2 2 32
A. a2 2, a3 B. a2 2, a3 C. 16 a2 , a3 D. , a3
 3 3 3 2 3
Câu 41. Cho một hình trụ có bán kính R = a. mặt phẳng P đi qua trục và cắt hình trụ theo một thiết 
diện có diện tích bằng 6a2 . Diện tích xung quanh của hình trụ và thể tích của khối trụ lần lượt là A. 8 a2 , 3 a3 B. 6 a2 , 6 a3 C. 6 a2 , 3 a3 D. 6 a2 , 9 a3
Câu 42. Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, có SA vuông góc với mặt phẳng (ABC) và có 
SA a, AB b, AC c . Mặt cầu ngoại tiếp hình chóp có bán kính r bằng:
 2 a2 b2 c2
 A. a b c B. 2 a2 b2 c2 C. D. a2 b2 c2 
 3 2
Câu 43. Trong không gian Oxyz cho điểm B 0;3;7 và I 12;5;0 . Tìm điểm A sao cho I là trung điểm của 
đoạn AB.A. (2;5;-5)B. (0;1;-1)C. (24;7;-7)D. (1;2;-5)
Câu 44. Tìm điểm M ở trên trục Ox và cách đều hai mặt phẳng x 2y 2z 1 0 và 2x 2y z 5 0 
 A. 4;0;0 B. 7;0;0 C. 6;0;0 D. 6;0;0 
Câu 45. Viết phương trình mặt phẳng đi qua 3 điểm A(1;-3;0), B(-2;9;7), C(0;0;1)
 A. 9x 4y 9z 7 0 B. 9x 4y 3z 3 0 C. 9x 4y 9z 9 0 D. 9x 4y 9z 9 0 
Câu 46. Mặt phẳng 2x 5y z 1 0 nhận vecto nào sau đây là vectơ pháp tuyến:
 A. n (-4;10;2) B. n (2;5;1) C. n (-2;5;-1) D. n (-2;-5;1)
Câu 47. Tính thể tích tứ diện OABC với A, B, C lần lượt là giao điểm của mặt phẳng 2x 3y 5z 30 0 với 
trục Ox, Oy, Oz. A. 78B. 120 C. 91D. 150
Câu 48. Viết phương trình mặt cầu tâm I 1;4; 7 tiếp xúc với mặt phẳng 6x 6y 7z 42 0 
 2 2 2 3 2 2 2
 A. x 5 y 3 z 1 B. x 1 y 3 z 3 1 
 4
 C. x 1 2 y 4 2 z 7 2 121 D. x 1 2 y 2 2 z 2 2 9 
Câu 49. Cho mặt cầu (S) có phương trình x2 y2 z2 4x 2y 2z 5 0 và mặt phẳng 
(P) :3x 2y 6z m 0 . (S) và (P) có giao nhau khi:
 A. m 9 hoặc m 5 B. 5 m 9 C. 2 m 3 D. m 3 hoặc m 2 
Câu 50. Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD với A 1;1;0 , B 1;0;1 , C 0;1;1 , D 1;2;3 
 A. x2 y2 x2 3x 3y 3z 6 0 B. x2 y2 x2 3x 3y 3z 5 0 
 C. x2 y2 x2 3x 3y 3z 4 0 D. x2 y2 x2 3x 3y 3z 3 0 
 HẾT.