Đề thi thử Tốt nghiệp THPT môn Toán - Năm học 2024 - Trường THPT Lý Tự Trọng (Có ma trận và đáp án)

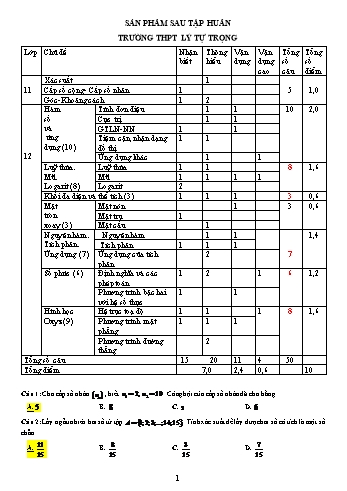
 SẢN PHẨM SAU TẬP HUẤN
 TRƯỜNG THPT LÝ TỰ TRỌNG
 Lớp Chủ đề Nhận Thông Vận Vận Tổng Tổng 
 biết hiểu dụng dụng số số 
 cao câu điểm
 Xác suất 1
 11 Cấp số cộng- Cấp số nhân 1 5 1,0
 Góc-Khoảng cách 1 2
 Hàm Tính đơn điệu 1 1 10 2,0
 số Cực trị 1 1
 và GTLN-NN 1 1
 ứng Tiệm cận, nhận dạng 1 1
 dụng (10) đồ thị
 12 Ứng dụng khác 1 1
 Luỹ thừa. Luỹ thừa 1 1 8 1,6
 Mũ. Mũ 1 1 1 1
 Logarit (8) Logarit 2
 Khối đa diện và thể tích (3) 1 1 1 3 0,6
 Mặt Mặt nón 1 3 0,6
 tròn Mặt trụ 1
 xoay (3) Mặt cầu 1
 Nguyên hàm. Nguyên hàm 1 1 1,4
 Tích phân. Tích phân 1 1 1
 Ứng dụng (7) Ứng dụng của tích 2 7
 phân
 Số phức (6) Định nghĩa và các 1 2 1 6 1,2
 phép toán
 Phương trình bậc hai 1 1
 với hệ số thực
 Hình học Hệ trục toạ độ 1 1 1 8 1,6
 Oxyz (9) Phương trình mặt 1 1 1
 phẳng
 Phương trình đường 2
 thẳng
 Tổng số câu 15 20 11 4 50
 Tổng điểm 7,0 2,4 0,6 10
Câu 1: Cho cấp số nhân un , biết u1 2, u2 10 . Công bội của cấp số nhân đã cho bằng
 A.5 . B. 8 .C. 2 .D. 6 .
Câu 2: Lấy ngẫu nhiên hai số từ tập A 1;2;3;...;14;15 . Tính xác suất để lấy được hai số có tích là một số 
chẵn.
 11 8 3 7
 A. . B. . C. . D. .
 15 15 15 15
 1 Câu 3: Cho hình chóp S.ABC có SA, SB, SC bằng nhau và đôi một vuông góc. Góc giữa đường thẳng AB và 
mặt phẳng SBC bằng
 A
 S C
 B
 A. 450 . B. 300 . C. 600 . D. 900 .
Câu 4: Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh 2a , SA a 6 và SA vuông góc với đáy. 
Góc giữa mặt phẳng SBD và mặt phẳng ABCD bằng
 S
 B
 A
 D C
A. 600 . B. 300 . C. 450 . D. 900 .
Câu 5: Cho lăng trụ đứng ABC.A B C , đáy ABC là tam giác đều có cạnh bằng 4 . Tính khoảng cách giữa hai 
đường thẳng AA và BC .
 A' C'
 B'
 A C
 B
A. 2 3 . B. 3 . C. 3 3 . D. 4 .
Câu 6: Cho hàm số y f x liên tục trên đoạn 1;4 và có đồ thị như hình vẽ sau. Gọi M , m lần lượt là giá 
  
trị lớn nhất, nhỏ nhất của hàm số trên đoạn  1;4. Tính M 2m .
 2 A. 1. B. 1. C. 5 . D. 5 .
 2x 1
Câu 7: Đường tiệm cận đứng của đồ thị hàm số y có phương trình là
 x 1 
 A. x 1. B. y 1. C. x 2 . D. y 2.
Câu 8: Hàm số y x2 2x đồng biến trên khoảng nào?
 A. 0; . B. 1; . C. ;0 . D. ; 1 .
 3
Câu 9: Cho hàm số y f x liên tục trên ¡ và có f x x2 x 1 x 2 x 3 . Số điểm cực tiểu của hàm 
số y f x là
 A. 2. B. 1. C. 3. D. 0.
Câu 10: Đồ thị sau đây là của hàm số nào?
 A. y x3 3x2 4 . B. y x3 3x2 4 . C. y x3 3x2 4 . D. y x3 3x2 4.
Câu 11: Cho hàm số y f x có bảng biến thiên như hình dưới.
Tập nghiệm của phương trình f x 1 có bao nhiêu phần tử?
 3 A. 3 . B. 4 . C. 2 . D. 1 .
 1
Câu 12: Tập xác định của hàm số y x 5 3 là
 A. 5; . B. 5; . C. ¡ . D. ¡ \ 5 .
 x
 x x 2 
Câu 13: Trong các hàm số: y 2024 , y e , y , có bao nhiêu hàm số đồng biến trên ¡ ?
 A. 2 . B. 3 . C. 0 . D. 1 .
Câu 14: Tập nghiệm của bất phương trình log 2 2x log 2 2 là
 3 3
A.  ;1 . B. 1; . C. 1; . D. 0;1.
Câu 15: Với a , b là các số thực dương tùy ý thỏa mãn a 1 và , giá trị của log a2b bằng
 loga b 8 a3 
 10 3 2 4
 A. . B. . C. . D. .
 3 2 3 3
Câu 16: Cho số thực x dương, biểu thức P 4 x 3 x x bằng
 3 13 5 11
 A. x8 . B. x12 . C. x12 . D. x 24 .
 2
Câu 17: Có bao nhiêu giá trị nguyên thuộc khoảng 10;10 của tham số m , để phương trình 3x 1 m có 
nghiệm?
 A. 7. B. 9. C. 10. D. 8.
Câu 18: Cho khối hộp có chiều cao bằng 2 , diện tích đáy bằng 6 . Thể tích của khối hộp đã cho bằng
 A. 12. B. 4 . C. 3. D. 8.
Câu 19: Cho khối chóp S.ABC có thể tích bằng V . Các điểm M , N, P lần lượt thuộc các cạnh SA, SB, SC 
sao cho MS MA, NS 2NB, PS 3PC . Thể tích khối chóp S.MNP bằng
 S
 A C
 B
 V V V V
 A. .B. . C. .D. .
 4 6 24 12
Câu 20: Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh 2a , SA vuông góc với đáy. Gọi M, N, P 
lần lượt là hình chiếu của A lên SB, SC, SD. Diện tích mặt cầu đi qua 7 điểm A, B, C, D, M, N, P bằng
 4 S
 B
 A
 D C
 8 a2 16 2 a2
A. 8 a2 . B. . C. 4 a2 . D. .
 3 3
A. 36 . B. 20 . C. 28 .D. 40 .
Câu 21: Cho khối trụ có thể tích bằng 25 và diện tích một đáy bằng 15. Chiều cao của khối trụ đã cho bằng
 5 5 
A. . B. . C. 5 . D. 5 .
 3 3
 1
Câu 22: Trên khoảng 0; , cho hàm số f (x) e x và C là một số thực bất kỳ. Khẳng định nào dưới 
 x
đây đúng?
 A. f (x)dx ln x e x C . B. f (x)dx ln x e x C .
 1 1
 C. f (x)dx e x C . D. f (x)dx e x C .
 x2 x2
 1 3 3 3
Câu 23: Nếu f x dx 2 , f x dx 3 , g x dx 10 thì f x 2g x dx bằng
 0 1 0 0
 A. 25 . B. 15. C. 12. D. 20 .
 x
Câu 24: Trên khoảng 0; , hàm số F(x) 10x cos x2 là một nguyên hàm của hàm số nào sau đây?
 2
 1 x x
A. f x 10x.ln10 sin 2x . B. f x 10x.ln10 sin 2x .
 2 2 2
 10x x x3 1 x
C. f x 2sin . D. f x 10x.ln10 sin 2x .
 ln10 2 3 2 2
Câu 25: Cho hàm số y f x liên tục trên  2;4 và có đồ thị (là một đoạn thẳng và một nửa đường tròn) 
 4
trên  2;4như hình vẽ. Tích phân f x dx bằng
 2
 5 Câu 26: Trong không gian Oxyz , một vật thể  nằm giữa hai mặt phẳng : x 1,  : x 1. Cắt vật thể 
  bởi một mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x 1 x 1 được thiết diện là hình 
tròn có bán kính bằng 5 . Thể tích của vật  thể bằng
 A. 10 . B. 5 2 . C. 10 2 . D. 5 .
Câu 27: Cho số phức z 2 i . Điểm nào sau đây biểu diễn số phức z ?
A. M 2;1 . B. M 2; 1 . C. M 2; 1 . D. M 2;1 .
 2
Câu 28: Biết số phức z0 là nghiệm của phương trình 2z z 2024 0 . Tính modun của số phức z0 .
A. 1012 . B. 2024 . C. 1012. D. 2024 .
Câu 29: Tìm phần ảo của số phức z , biết z 1 i 101 .
A. 250 . B. 250 i . C. 250 . D. 250 i .
Câu 30: Cho hai số phức z và w thoả mãn z 1, w 2z 3. Chọn khẳng định sai?
A. Tập hợp điểm biểu diễn số phức w là một đường tròn có bán kính R 3 . 
 B. Tập hợp điểm biểu diễn số phức w là một đường tròn. 
C. Tập hợp điểm biểu diễn số phức w là một đường tròn có tâm thuộc trục hoành. 
D. Tập hợp điểm biểu diễn số phức w là một đường tròn bán kính R 2 . .
Câu 31: Trong không gian Oxyz , cho hai vectơ u 1;2; 2 và v 2; 2;3 . Tọa độ của vectơ u v là
 A. 1;4; 5 . B. 1; 4;5 . C. 3;0;1 . D. 3;0; 1 .
Câu 32: Trong không gian Oxyz , cho hai điểm A 1;4;2 , B 1;2;0 . Mặt cầu đường kính AB có phương 
trình là
 A. x2 y 3 2 z 1 2 3 . B. x2 y 3 2 z 1 2 12 .
 C. x 1 2 y 1 2 z 1 2 3 . D. x 1 2 y 1 2 z 1 2 12 .
Câu 33: Trong không gian Oxyz , cho mặt phẳng P : 2x 2y z 9 0 và điểm I 1; 1; 10 . Gọi Q là 
mặt phẳng song song với mặt phẳng P , đồng thời khoảng cách từ điểm I đến mặt phẳng Q bằng 1. 
Phương trình mặt phẳng Q là
A. P : 2x 2y z 3 0 . B. P : 2x 2y z 9 0 .
C. P : 2x 2y z 9 0 . D. P : 2x 2y z 3 0 .
Câu 34: Trong không gian Oxyz , cho mặt phẳng P đi qua điểm A 4; 1;2 và nhận n 3;0;1 là một véc tơ 
pháp tuyến. Phương trình mặt phẳng P là
 A. 3x z 14 0 . B. 4x y 2z 14 0 . C. 3x y 14 0 . D. 4x y 2z 14 0.
 6 Câu 35: Trong không gian Oxyz , cho mặt phẳng P đi qua các điểm A 3;0;0 , B 0;3;0 , C 0;0; 6 . 
Đường thẳng d đi qua trọng tâm G của tam giác ABC và vuông góc với mặt phẳng ABC , phương trình 
của đường thẳng d là
 x 1 y 1 z 2 x 1 y 1 z 2
A. . B. .
 2 2 1 2 2 1
 x 1 y 1 z 2 x 1 y 1 z 2
C. . D. .
 3 3 6 3 3 6
 x 1 t
Câu 36: Trong không gian Oxyz , cho đường thẳng d : y 2 2t . Đường thẳng d ' nằm trong mặt 
 z 1 3t
phẳng Oxy , vuông góc với đường thẳng d , một véc tơ chỉ phương của đường thẳng d ' là
A. u 2;1;0 . B. u 3; 3;3 . C. u 2;1;0 . D. u 2; 1;0 .
PHẦN VẬN DỤNG
Câu 1: Cho hàm số y f (x) có đồ thị f (x) như hình vẽ sau
 1
 Biết f 0 0. Hỏi hàm số g x f x3 2x có bao nhiêu điểm cực trị
 3 
 A. 1. B. 3. C. 4 . D. 5 .
 Lời giải
 Chọn B
 1
 Đặt h x f x3 2x h x x2 f x3 2
 3 
 2
 Ta có h x 0 f x3 , x 0 , 1 
 x2
 Đặt t x3 x 3 t
 2
 Từ 1 ta có: f t , 2 
 3 t2
 7 2 4 1
 Đặt m t m t .
 3 t2 3 3 t5
 Lúc này ta có hình vẽ 2 đồ thị như sau
 3
 Suy ra pt 2 có 1 nghiệm t t0 0 pt 1 có nghiệm x t0 x0 0
 Bảng biến thiên của h x , g x h x như sau
 Vậy hàm số y g x có 3 điểm cực trị.
Câu 2: Cho hàm số f x x3 ax2 bx 2 thỏa mãn min f x f 2 2 . Tích các giá trị thực của tham số 
 0;3 
 m để giá trị lớn nhất của hàm số y f x m trên đoạn 0;3 bằng 10 là
 A. 64 . B. 32 . C. 32 . D. 64 .
 Lời giải
 Ta có f x 3x2 2ax b .
 8 f 2 0 12 4a b 0 a 3
 Vì min f x f 2 2 suy ra .
 0;3 f 2 2 10 4a 2b 2 b 0
 Khi đó f x x3 3x2 2 .
 Xét hàm số g x f x m x3 3x2 2 m với x 0;3.
 2 x 0
 Ta có g x 3x 6x g x 0 .
 x 2
 Ta có g 0 m 2 , g 2 m 2 , g 3 m 2 . Do đó max g x m 2 , min g x m 2 .
 0;3 0;3
Câu 3: Cho hàm số y f x có đồ thị y f x như hình vẽ 
 Bất phương trình f 4sin x 4sin2 x m 0 có nghiệm x 0; khi và chỉ khi
 A. m f 0 . B. m f 4 4 .C. m f 0 . D. m f 4 4 .
 Lời giải
 1
Đặt 4sin x t t 0;4 ta được BPT m f t t 2 có nghiệm t 0;4.
 4
 1 t
Xét g t f t t 2 với t 0;4. g t f t .
 4 2
 t
 g t 0 f t .
 2
 t 0 4
 g t 
 g 0 
 g t 
 g 4 
Vậy BPT m g t có nghiệm t 0;4 khi và chỉ khi m g 0 m f 0 .
Câu 4: Cho hàm số đa thức bậc ba y f x có đồ thị của các hàm số y f x và y f x như hình vẽ.
 9 Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f f x m 2 f x 3 x m có đúng 3 
nghiệm thực. Tổng các phần tử của S bằng
 A. .0 B. .C. 6 5 .D. 7 .
 Lời giải
 Dựa vào đồ thị, ta có: f x ax x 2 a x2 2x .
 Vì f 1 3 a 3 a 3 . Lúc đó: f x 3x2 6x . Suy ra: f x x3 3x2 c .
 .Vì f 1 0 1 3 c 0 c 2 . Lúc đó: f x x3 3x2 2 .
 Theo đề: f f x m 2 f x 3 x m f f x m 3 f x 3m f x 3x 
 f f x m 3 f x m f x 3x (*)
 Xét hàm số g u f u 3u trên ¡ .
 2
 g u f u 3 3u2 6u 3 3 u 1 0,u ¡ .
 Nên g u là hàm số đồng biến trên ¡ .
 Do đó: (*) f x m x m f x x .
 Xét hàm số y h x f x x x3 3x2 x 2 trên ¡ .
 3 2 3
 x 
 2 3
 h x 3x 6x 1. Do đó: h x 0 .
 3 2 3
 x 
 3
 Bảng biến thiên: 
 Phương trình f f x m 2 f x 3 x m có đúng 3 nghiệm thực
 9 16 3 9 16 3
 Phương trình m f x x có 3 nghiệm thực m 
 9 9
 Vì m là số nguyên nên m 4; 3; 2; 1; 0;1;2 .
Do đó: S 4 3 2 1 0 1 2 7 .
 10