Trắc nghiệm Toán Lớp 12 - Chủ đề 3: Nguyên hàm. Tích phân - Trường THPT Đoàn Kết

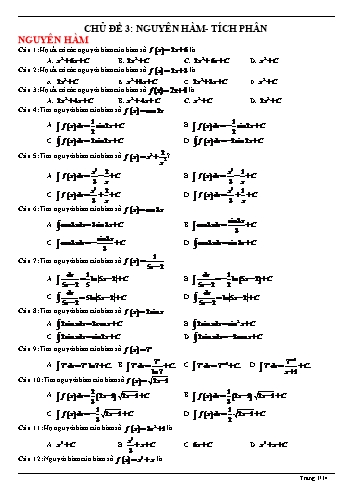
 CHỦ ĐỀ 3: NGUYÊN HÀM- TÍCH PHÂN
NGUYÊN HÀM
Câu 1: Họ tất cả các nguyên hàm của hàm số f x 2x 6 là
 A. x2 6x C . B. 2x2 C . C. 2x2 6x C . D. x2 C .
Câu 2: Họ tất cả các nguyên hàm của hàm số f x 2x 3 là 
 A. 2x2 C .B. x2 3x C .C. 2x2 3x C .D. x2 C .
Câu 3: Họ tất cả các nguyên hàm của hàm số f (x) 2x 4 là
 A. 2x2 4x C . B. x2 4x C . C. x2 C . D. 2x2 C .
Câu 4: Tìm nguyên hàm của hàm số f x cos 2x . 
 1 1
 A. f x dx sin 2x C . B. f x dx sin 2x C . 
 2 2
 C. f x dx 2sin 2x C . D. f x dx 2sin 2x C . 
 2
Câu 5: Tìm nguyên hàm của hàm số f x x2 ?
 x2
 x3 2 x3 1
 A. f x dx C . B. f x dx C .
 3 x 3 x
 x3 2 x3 1
 C. f x dx C . D. f x dx C .
 3 x 3 x
Câu 6: Tìm nguyên hàm của hàm số f x cos3x .
 sin 3x
 A. cos3xdx 3sin 3x C .B. cos3xdx C .
 3
 sin 3x
 C. cos3xdx C . D. cos3xdx sin 3x C .
 3 
 1
Câu 7: Tìm nguyên hàm của hàm số f x 
 5x 2
 dx 1 dx 1
 A. ln 5x 2 C . B. ln 5x 2 C .
 5x 2 5 5x 2 2
 dx dx
 C. 5ln 5x 2 C . D. ln 5x 2 C .
 5x 2 5x 2
Câu 8: Tìm nguyên hàm của hàm số f x 2sin x .
 A. 2sin xdx 2cos x C . B. 2sin xdx sin2 x C .
 C. 2sin xdx sin 2x C .D. 2sin xdx 2cos x C .
Câu 9: Tìm nguyên hàm của hàm số f x 7x .
 7x 7x 1
 A. 7x dx 7x ln 7 C. B. 7x dx C. C. 7x dx 7x 1 C. D. 7x dx C.
 ln 7 x 1
Câu 10: Tìm nguyên hàm của hàm số f x 2x 1 .
 2 1
 A. f x dx 2x 1 2x 1 C . B. f x dx 2x 1 2x 1 C . 
 3 3
 1 1
 C. f x dx 2x 1 C . D. f x dx 2x 1 C .
 3 2
Câu 11: Họ nguyên hàm của hàm số f x 3x2 1 là
 x3
 A. x3 C . B. x C . C. 6x C .D. x3 x C .
 3
Câu 12: Nguyên hàm của hàm số f x x3 x là 
 Trang 1/14 2
 1 1
 A. x4 x2 C . B. 3x2 1 C . C. x3 x C .D. x4 x2 C .
 4 2
Câu 13: Nguyên hàm của hàm số f x x4 x là
 1 1
 A. x4 x C . B. 4x3 1 C . C. x5 x2 C .D. x5 x2 C .
 5 2
Câu 14: Nguyên hàm của hàm số f x x4 x2 là
 1 1
 A. 4x3 2x C .B. x5 x3 C . C. x5 x3 C . D. x4 x2 C .
 5 3
Câu 15: Nguyên hàm của hàm số f x x3 x2 là
 1 1
 A. 3x2 2x C .B. x4 x3 C . C. x4 x3 C . D. x3 x2 C .
 4 3
Câu 16: Họ nguyên hàm của hàm số f x ex x là
 1 1 1
 A. ex x2 C .B. ex x2 C . C. ex x2 C . D. ex 1 C .
 2 x 1 2
Câu 17: Họ nguyên hàm của hàm số f x 4x 1 ln x là
 A. 2x2 ln x 3x2 . B. 2x2 ln x x2 . C. 2x2 ln x 3x2 C .D. 2x2 ln x x2 C .
Câu 18: Họ tất cả các nguyên hàm của hàm số f x 2x 5 là:
 A. x2 5x C . B. 2x2 5x C . C. 2x2 C . D. x2 C .
 3
Câu 19: Cho F x là một nguyên hàm của hàm số f x ex 2x thỏa mãn F 0 . Tìm F x .
 2
 3 1 5 1
A. F x ex x2 . B. F x 2ex x2 . C. F x ex x2 . D. F x ex x2 .
 2 2 2 2
Câu 20: Tìm nguyên hàm F x của hàm số f x sin x cos x thoả mãn F 2
 2 
 A. F x cos x sin x 3 .B. F x cos x sin x 3.
 C. F x cos x sin x 1. D. F x cos x sin x 1.
 ln x
Câu 21: Cho F x là nguyên hàm của hàm số f x . Tính F e F 1 .
 x
 1 1
 A. I e . B. I .C. I . D. I 1.
 e 2
 1
Câu 22: Biết F x là một nguyên hàm của f x và F 2 1. Tính F 3 . 
 x 1
 1 7
 A. F 3 ln 2 1. B. F 3 ln 2 1. C. F 3 . D. F 3 .
 2 4
Câu 23: Cho hàm số f x thỏa mãn f x 3 5sin x và f 0 10 . Mệnh đề nào dưới đây là đúng?
 A. f x 3x 5cos x 5 . B. f x 3x 5cos x 2 .
 C. f x 3x 5cos x 2. D. f x 3x 5cos x 15 .
 1  2
Câu 24: Cho hàm số f x xác định trên ¡ \  thỏa mãn f x , f 0 1 và f 1 2 . Giá trị của 
 2 2x 1
 biểu thức f 1 f 3 bằng
 A. 4 ln15 . B. 2 ln15 .C. 3 ln15. D. ln15.
 3x 1
Câu 25: Họ tất cả các nguyên hàm của hàm số f (x) trên khoảng (1; ) là
 (x 1)2
 2 1
 A. 3ln(x 1) C . B. 3ln(x 1) C .
 x 1 x 1
 Trang 2/14 1 2
 C. 3ln(x 1) C . D. 3ln(x 1) C .
 x 1 x 1
 2x 1
Câu 26: Họ tất cả các nguyên hàm của hàm số f x trên khoảng 2; là:
 x 2 2
 1 1
 A. 2ln x 2 C . B. 2ln x 2 C .
 x 2 x 2
 3 3
 C. 2ln x 2 C . D. 2ln x 2 C .
 x 2 x 2
 3x 2
Câu 27: Họ tất cả các nguyên hàm của hàm số f x trên khoảng 2; là
 x 2 2
 4 2
 A. 3ln x 2 C . B. 3ln x 2 C .
 x 2 x 2
 2 4
 C. 3ln x 2 C . D. 3ln x 2 C .
 x 2 x 2
 2x 1
Câu 28: Họ tất cả các nguyên hàm của hàm số f x trên khoảng 1; là
 x 1 2
 2 3
 A. 2ln x 1 C .B. 2ln x 1 C .
 x 1 x 1
 2 3
 C. 2ln x 1 C . D. 2ln x 1 C .
 x 1 x 1
 1 f x 
Câu 29: Cho F x là một nguyên hàm của hàm số . Tìm nguyên hàm của hàm số f x ln x .
 2x2 x
 ln x 1 ln x 1
 A. f x ln xdx 2 2 C . B. f x ln xdx 2 2 C .
 x 2x x x
 ln x 1 ln x 1
 C. f x ln xdx 2 2 C . D. f x ln xdx 2 2 C .
 x x x 2x
Câu 30: Cho F x x 1 ex là một nguyên hàm của hàm số f x e2x . Tìm nguyên hàm của hàm số 
 f x e2x .
 2 x
 A. f x e2xdx (4 2x)ex C . B. f x e2xdx ex C .
 2
 C. f x e2xdx 2 x ex C . D. f x e2xdx x 2 ex C .
 1 f x 
Câu 31: Cho F x là một nguyên hàm của hàm số . Tìm nguyên hàm của hàm số f x ln x .
 3x3 x
 ln x 1 ln x 1
 A. f x ln xdx C . B. f x ln xdx C .
 x3 5x5 x3 5x5
 ln x 1 ln x 1
 C. f x ln xdx C . D. f x ln xdx C .
 x3 3x3 x3 3x3
 2 2
Câu 32: Cho hàm số f x thỏa mãn f 2 và f x 2x f x với mọi x ¡ . Giá trị của f 1 
 9 
 bằng
 35 2 19 2
 A. .B. . C. . D. .
 36 3 36 15
 1 2
Câu 33: Cho hàm số f x thỏa mãn f 2 và f x x f x với mọi x ¡ . Giá trị của f 1 bằng
 3 
 11 2 2 7
 A. .B. . C. . D. .
 6 3 9 6
 Trang 3/14 4
 1 2
Câu 34: Cho hàm số f x thỏa mãn f 2 và f x 4x3 f x với mọi x R . Giá trị của f 1 
 25 
 bằng 
 1 41 1 391
 A. . B. . C. . D. .
 10 400 40 400
 1 2
Câu 35: Cho hàm số f x thỏa mãn f 2 và f x x3 f x với mọi x ¡ . Giá trị của f 1 bằng
 5 
 4 79 4 71
 A. . B. .C. . D. .
 35 20 5 20
TÍCH PHÂN
 2
Câu 36: e3x 1dx bằng
 1
 1 1 1
 A. e5 e2 . B. e5 e2 . C. e5 e2 . D. e5 e2 .
 3 3 3
 1 1 1
Câu 37: Biết f x dx 3 và g x dx 4 khi đó f x g x dx bằng
 0 0 0
 A. 7 . B. 7 . C. 1. D. 1.
 2 2 2
 f x dx 2 g x dx 6 f x g x dx
Câu 38: Biết 1 và 1 , khi đó 1 bằng
 A. 4 . D. 8 . C. 8 . D. 4.
 1 1 1
 f x dx 2 g x dx 4  f x g x dx
Câu 39: Biết 0 và 0 , khi đó 0 bằng
 A. 6 . B. 6 . C. 2 . D. 2 .
 2
Câu 40: Cho hàm số f x có đạo hàm trên đoạn 1;2, f 1 1 và f 2 2 . Tính I f x dx
 1
 7
 A. I 1. B. I 1. C. I 3 . D. I .
 2
 2 2 2
Câu 41: Cho f x dx 2 và g x dx 1. Tính I x 2 f x 3g x dx
 1 1 1
 5 7 17 11
 A. I . B. I .C. I . D. I .
 2 2 2 2
 2 2
Câu 42: Cho f x dx 5 . Tính I f x 2sin x dx .
 0 0
 A. I 7 . B. I 5 . C. I 3 . D. I 5 .
 2
 e
Câu 43: Tính tích phân I x ln xdx :
 1
 1 e2 2 e2 1 e2 1
 A. I . B. I .C. I . D. I .
 2 2 4 4
 2
Câu 44: Tính tích phân I 2x x2 1dx bằng cách đặt u x2 1, mệnh đề nào dưới đây đúng?
 1
 2 2 3 1 2
 A. I 2 udu. B. I udu. C. I udu. D. I udu.
 0 1 0 2 1
 1 dx 1 e
Câu 45: Cho a bln , với a , b là các số hữu tỉ. Tính S a3 b3 .
 x
 0 e 1 2
 Trang 4/14 A. S 2 . B. S 2 .C. S 0 . D. S 1. 
 6 2
Câu 46: Cho f x dx 12 . Tính I f 3x dx .
 0 0
 A. I 6 . B. I 36 . C. I 2 .D. I 4 .
 1 1 1 
Câu 47: Cho dx a ln 2 bln 3 với a , b là các số nguyên. Mệnh đề nào dưới đây đúng?
 0 x 1 x 2 
 A. a b 2 . B. a 2b 0. C. a b 2 .D. a 2b 0 .
Câu 48: Tính tích phân I cos3 x.sin xdx .
 0
 1 1
 A. I 4 . B. I 4 .C. I 0 . D. I .
 4 4
 4 2
Câu 49: Cho f x dx 16 . Tính tích phân I f 2x dx.
 0 0
 A. I 32 .B. I 8 . C. I 16 . D. I 4 .
 4 dx
Câu 50: Biết I a ln 2 bln 3 c ln 5 , với a , b , c là các số nguyên. Tính S a b c.
 2
 3 x x
 A. S 6 .B. S 2 . C. S 2 . D. S 0.
 2 dx
Câu 51: Tích phân bằng
 0 x 3
 16 5 5 2
 A. . B. log .C. ln . D. .
 225 3 3 15
 1
Câu 52: e3x 1dx bằng
 0
 1 1
 A. e4 e . B. e4 e . C. e4 e . D. e3 e .
 3 3
 2 dx
Câu 53: bằng
 1 3x 2
 1 2
 A. 2ln 2 . B. ln 2. C. ln 2 .D. ln 2 .
 3 3
 2 dx
Câu 54: . bằng
 1 2x 3
 5 1 7 1 7
 A. 2ln .B. ln . C. ln 35 . D. ln .
 7 2 5 2 5
 55 dx
Câu 55: Cho a ln 2 bln 5 c ln11 với a , b , c là các số hữu tỉ. Mệnh đề nào dưới đây đúng?
 16 x x 9
 A. a b c . B. a b c . C. a b 3c . D. a b 3c .
 21 dx
Câu 56: Cho a ln 3 bln 5 c ln 7 , với a , b , c là các số hữu tỉ. Mệnh đề nào sau đây đúng?
 5 x x 4
 A. a b 2c . B. a b c . C. a b c . D. a b 2c .
 e
Câu 57: Cho 1 x ln x dx ae2 be c với a , b , c là các số hữu tỉ. Mệnh đề nào dưới đây đúng?
 1
 A. a b c . B. a b c . C. a b c .D. a b c .
 e
Câu 58: Cho 2 x ln x dx a.e2 b.e c với a , b , c là các số hữu tỉ. Mệnh đề nào dưới đây đúng?
 1
 A. a b c . B. a b c .C. a b c . D. a b c .
 Trang 5/14 6
 1 1 1
Câu 59: Cho f x dx 2 và g x dx 5 khi đó f x 2g x dx bằng
 0 0 0
 A. 3 . B. 12.C. 8 . D. 1.
 1 xdx
Câu 60: Cho a bln 2 c ln 3 với a , b , c là các số hữu tỷ. Giá trị của3 a b c bằng
 2
 0 x 2 
 A. 2 .B. 1. C. 2 . D. 1.
 1 1 1
Câu 61: Biết f x dx 2 và g x dx 3, khi đó f x g x dx bằng
 0 0 0
 A. 5 . B. 5 . C. 1. D. 1.
 4
Câu 62: Cho hàm số f x . Biết f 0 4 và f '(x) 2cos2 x 3,x ¡ , khi đó f (x)dx bằng
 0
 2 2 2 8 8 2 8 2 2 6 8
 A. . B. . C. . D. .
 8 8 8 8
 1 5
Câu 63: Cho hàm số f x có đạo hàm liên tục trên ¡ . Biết f 5 1 và xf 5x dx 1, khi đó x2 f x dx 
 0 0
 bằng
 123
 A. 15. B. 23. C. . D. 25 .
 5
 f x f 0 4 f x 2sin2 x 1 4
Câu 64: Cho hàm số . Biết và , x ¡ , khi đó f x dx bằng
 0
 2 15 2 16 16 2 16 4 2 4
 A. . B. . C. . D. .
 16 16 16 16
 1
Câu 65: Cho hàm số f (x) có đạo hàm và liên tục trên ¡ , biết f (6) 1 và xf (6x)dx 1. Khi đó 
 0
 6
 x2 f '(x)dx ?
 0
 107
 A. B. 34 C. 24 D. 36
 3
 4
Câu 66: Cho hàm số y f x . Biết f 0 4 và f x 2sin2 x 3 , x ¡ . Khi đó f x dx bằng 
 0
 2 2 2 8 8 2 8 2 3 2 2 3
 A. . B. . C. . D. .
 8 8 8 8
 1
Câu 67: Cho hàm số f (x) có đạo hàm và liên tục trên ¡ , biết f (3) 1 và xf (3x)dx 1. Khi đó 
 0
 3
 x2 f '(x)dx ?
 0
 25
 A. 3B. 7 C. 9 D. 
 3
 1 1
Câu 68: Cho hàm số f x thỏa mãn x 1 f x dx 10 và 2 f 1 f 0 2 . Tính f x dx .
 0 0
 A. I 12 . B. I 8 . C. I 1. D. I 8 .
Câu 69: Cho hàm số f x liên tục trên ¡ và thỏa mãn f x f x 2 2cos 2x, x ¡ . Tính 
 Trang 6/14 3 
 2
 I f x d x 
 3 
 2
 A. I 6 . B. I 0 . C. I 2 . D. I 6 . 
 2 dx
Câu 70: Biết I a b c với a , b , c là các số nguyên dương. Tính P a b c .
 1 x 1 x x x 1
 A. P 24 . B. P 12. C. P 18.D. P 46 .
 1
 2
Câu 71: Cho hàm số f x có đạo hàm liên tục trên đoạn 0;1 thỏa mãn f 1 0, f x dx 7 và 
 0
 1 1 1
 x2 f x dx . Tích phân f x dx bằng
 0 3 0
 7 7
 A. . B. 1. C. . D. 4 .
 5 4
 4
Câu 72: Cho hàm số f x . Biết f 0 4 và f x 2cos2 x 1, x ¡ , khi đó f x dx bằng
 0
 2 4 2 14 2 16 4 2 16 16
 A. . B. .C. . D. .
 16 16 16 16
 1 4
Câu 73: Cho hàm số f x có đạo hàm liên tục trên ¡ . Biết f 4 1 và xf 4x dx 1, khi đó x2 f x dx 
 0 0
 bằng
 31
 A. .B. 16 . C. 8 . D. 14.
 2
ỨNG DỤNG TÍCH PHÂN
Câu 74: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi 
 đồ thị hàm số y f x , trục Ox và hai đường thẳng x a , x b a b , xung quanh trục Ox .
 b b b b
 A. V f 2 x dx . B. V f 2 x dx . C. V f x dx . D. V f x dx .
 a a a a
Câu 75: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y x3 x và đồ thị hàm số y x x2 . 
 37 9 81
 A. . B. I . C. . D. 13.
 12 4 12
Câu 76: Kí hiệu H là hình phẳng giới hạn bởi đồ thị hàm số y 2 x 1 ex , trục tung và trục hoành. Tính 
 thể tích V của khối tròn xoay thu được khi quay hình H xung quanh trục Ox :
 A. V 4 2e . B. V 4 2e . C. V e2 5 . D. V e2 5 .
Câu 77: Gọi S là diện tích hình phẳng H giới hạn bởi các đường y f x , trục hoành và hai đường thẳng 
 0 2
 x 1, x 2 . Đặt a f x dx , b f x dx , mệnh đề nào sau đây đúng?
 1 0
 y
 1
 O 2 x
 A. S b a . B. S b a . C. S b a . D. S b a .
Câu 78: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x 1 và x 3, biết rằng khi cắt vật thể 
 bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x 1 x 3 thì được thiết diện là 
 một hình chữ nhật có hai cạnh là 3x và 3x2 2 .
 Trang 7/14 8
 124 124
 A. V 32 2 15 . B. V .C. V . D. V 32 2 15 .
 3 3 
Câu 79: Cho hình phẳng D giới hạn bởi đường cong y 2 cos x , trục hoành và các đường thẳng x 0 , 
 x . Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
 2
 A. V 1. B. V 1 .C. V 1 . D. V 1.
Câu 80: Một vật chuyển động trong 3 giờ với vận tốc v phụ thuộc vào thời gian t có đồ thị vận tốc như hình 
 bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường 
 parabol có đỉnh I 2;9 và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là 
 một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di chuyển được trong 3 giờ 
 đó .
 y I
 9
 4
 O 1 2 3 t
 A. s 23,25 (km) .B. s 21,58 (km) . C. s 15,50 (km) . D. s 13,83 (km) .
Câu 81: Cho hình phẳng D giới hạn bởi đường cong y 2 sin x , trục hoành và các đường thẳng x 0 , 
 x . Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
 A. V 2 1 .B. V 2 1 . C. V 2 2 . D. V 2 .
Câu 82: Cho hình phẳng D giới hạn bởi đường cong y ex , trục hoành và các đường thẳng x 0 , x 1. Khối 
 tròn xoay tạo thanh khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
 2 2
 e2 e 1 e2 1 e 1 
 A. V . B. V . C. V .D. V .
 2 2 2 2
Câu 83: Cho hình phẳng D giới hạn với đường cong y x2 1, trục hoành và các đường thẳng x 0 , x 1. 
 Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
 4 4
 A. V . B. V 2 . C. V . D. V 2 .
 3 3
Câu 84: Một ô tô đang chạy với tốc độ 10 m/s thì người lái đạp phanh ; từ thời điểm đó, ô tô chuyển động 
 chậm dần đều với v t 5t 10 m/s , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt 
 đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
 A. 0,2 m . B. 2 m . C. 10 m . D. 20 m .
Câu 85: Cho hình thang cong H giới hạn bởi các đường y ex , y 0, x 0 , x ln 4 . Đường thẳng 
 x k (0 k ln 4) chia H thành hai phần có diện tích là S1 và S2 như hình vẽ bên. Tìm k để 
 S1 2S2 .
 y
 S 2
 S
 1 x
 O k l n 4
 2 8
 A. k ln 4 . B. k ln 2 . C. k ln .D. k ln 3.
 3 3
Câu 86: Ông An có một mảnh vườn hình elip có độ dài trục lớn bằng 16 m và độ dài trục bé bằng 10 m . Ông 
 muốn trồng hoa trên một dải đất rộng 8 m và nhận trục bé của elip làm trục đối xứng . Biết kinh phí 
 để trồng hoa là 100.000 đồng/1 m2 . Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó? .
 Trang 8/14 8m
 A. 7.862.000 đồng.B. 7.653.000 đồng. C. 7.128.000 đồng. D. 7.826.000 đồng.
Câu 87: Một vật chuyển động trong 3 giờ với vận tốc v phụ thuộc vào thời gian t có đồ thị là một phần của 
 đường parabol có đỉnh I(2;9) và trục đối xứng song song với trục tung như hình bên. Tính quãng 
 đường s mà vật di chuyển được trong 3 giờ đó.
 v I
 9
 6
 O 2 3 t
 A. s 24,25 (km) B. s 26,75 (km) C. s 24,75 (km) D. s 25,25 (km)
Câu 88: Cho hàm số y f x liên tục trên đoạn a;b. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số 
 y f x , trục hoành và hai đường thẳng x a , x b a b . Thể tích khối tròn xoay tạo thành khi 
 quay D quanh trục hoành được tính theo công thức.
 b b b b
 A. V f 2 x dx . B. V 2 f 2 x dx . C. V 2 f 2 x dx . D. V 2 f x dx .
 a a a a
Câu 89: Cho H là hình phẳng giới hạn bởi parabol y 3x2 , cung tròn có phương trình y 4 x2 và 
 trục hoành . Diện tích của H bằng
 y
 2
 O 2 x
 4 3 4 3 4 2 3 3 5 3 2 
 A. .B. . C. . D. .
 12 6 6 3
Câu 90: Gọi S là diện tích hình phẳng giới hạn bởi các đường y ex , y 0, x 0 , x 2 . Mệnh đề nào dưới 
 đây đúng?
 2 2 2 2
 A. S e2x dx .B. S ex dx . C. S ex dx . D. S e2x dx .
 0 0 0 0
Câu 91: Gọi S là diện tích của hình phẳng giới hạn bởi các đường y 2x , y 0, x 0 , x 2 . Mệnh đề nào 
 dưới đây đúng?
 2 2 2 2
 A. S 2x dx . B. S 22x dx . C. S 22x dx . D. S 2x dx .
 0 0 0 0
Câu 92: Cho hình phẳng H giới hạn bởi các đường y x2 3 , y 0, x 0 , x 2 Gọi V là thể tích khối 
 tròn xoay được tạo thành khi quay H xung quanh trục Ox . Mệnh đề nào sau đây đúng?
 Trang 9/14 10
 2 2 2 2
 2 2
 A. V x2 3 dx . B. V x2 3 dx .C. V x2 3 dx . D. V x2 3 dx .
 0 0 0 0
Câu 93: Cho hình phẳng H giới hạn bởi các đường y x2 2 , y 0, x 1, x 2 . Gọi V là thể tích của khối 
 tròn xoay được tạo thành khi quay H xung quanh trục Ox . Mệnh đề nào dưới đây đúng?
 2 2 2 2
 2 2
 A. V x2 2 dx . B. V x2 2 dx .C. V x2 2 dx . D. V x2 2 dx .
 1 1 1 1
Câu 94: Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật 
 1 11
 v t t 2 t m s , trong đó t là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ 
 180 18
 trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng cùng hướng với A nhưng 
 chậm hơn 5 giây so với A và có gia tốc bằng a m s2 ( a là hằng số). Sau khi B xuất phát được 10 
 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng 
 A. 22 m s .B. 15 m s . C. 10 m s . D. 7 m s .
Câu 95: Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật 
 1 59
 v t t 2 t m/s , trong đó t là khoảng thời gian tính từ lúc a bắt đầu chuyển động. Từ trạng 
 150 75
 thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng cùng hướng với A nhưng chậm 
 hơn 3 giây so với A và có gia tốc bằng a m/s2 ( a là hằng số). Sau khi B xuất phát được 12 giây 
 thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng
 A. 20 m/s .B. 16 m/s . C. 13 m/s . D. 15 m/s .
Câu 96: Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật 
 1 13
 v t t 2 t m/s , trong đó t là khoảng thời gian tính từ lúc A bắt đầu chuyển động Từ 
 100 30
 trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng cùng hướng với A nhưng 
 chậm hơn 10 giây so với A và có gia tốc bằng a m/s2 ( a là hằng số). Sau khi B xuất phát được 
 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng
 A. 25 m/s . B. 15 m/s . C. 9 m/s . D. 42 m/s .
Câu 97: Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật 
 1 58
 v t t 2 t m s , trong đó t là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ 
 120 45
 trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng cùng hướng với A nhưng 
 chậm hơn 3 giây so với A và có gia tốc bằng a m s2 ( a là hằng số). Sau khi B xuất phát được 
 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng 
 A. 21 m s . B. 36 m s .C. 30 m s . D. 25 m s .
 1
Câu 98: Cho hai hàm số f x ax3 bx2 cx và g x dx2 ex 1 ( a , b , c , d , e ¡ ). Biết rằng đồ 
 2
 thị của hàm số y f x và y g x cắt nhau tại ba điểm có hoành độ lần lượt là 3 ; 1; 1 . Hình 
 phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
 y
 1
 3 1O x
 9
 A. . B. 8 .C. 4 . D. 5 .
 2
 Trang 10/14