Chuyên đề Khối đa diện và thể tích khối đa diện - Chuyên đề 6: Khối đa diện và thể tích khối đa diện - Trường THPT Nguyễn Du

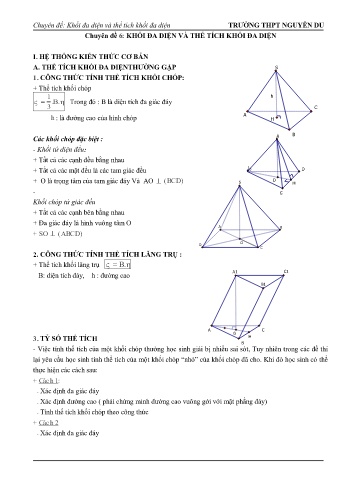
 Chuyên đề: Khối đa diện và thể tích khối đa diện TRƯỜNG THPT NGUYỄN DU 
 Chuyên đề 6: KHỐI ĐA DIỆN VÀ THỂ TÍCH KHỐI ĐA DIỆN 
I. HỆ THỐNG KIẾN THỨC CƠ BẢN 
A. THỂ TÍCH KHỐI ĐA DIỆNTHƯỜNG GẶP S
1. CÔNG THỨC TÍNH THỂ TÍCH KHỐI CHÓP: 
+ Thể tích khối chóp 
 1 h
V .. B h Trong đó : B là diện tích đa giác đáy 
 3 C
 A
 h : là đường cao của hình chóp H
 _A B
Các khối chóp đặc biệt : 
- Khối tứ diện đều: 
+ Tất cả các cạnh đều bằng nhau 
 _ 
+ Tất cả các mặt đều là các tam giác đều b _D 
 _O 
+ O là trọng tâm của tam giác đáy Và AO  (BCD) S _M 
- _C 
Khối chóp tứ giác đều 
+ Tất cả các cạnh bên bằng nhau 
+ Đa giác đáy là hình vuông tâm O 
 A B
+ SO (ABCD) 
 O
 D
 C
2. CÔNG THỨC TÍNH THỂ TÍCH LĂNG TRỤ : 
+ Thể tích khối lăng trụ V B. h 
 A1 C1
 B: diện tích đáy, h : đường cao 
 B1
 A C
 G
3. TỶ SỐ THỂ TÍCH H
 B
- Việc tính thể tích của một khối chóp thường học sinh giải bị nhiều sai sót, Tuy nhiên trong các đề thi 
lại yêu cầu học sinh tính thể tích của một khối chóp “nhỏ” của khối chóp đã cho. Khi đó học sinh có thể 
thực hiện các cách sau: 
+ Cách 1: 
 . Xác định đa giác đáy 
 . Xác định đường cao ( phải chứng minh đường cao vuông gới với mặt phẳng đáy) 
 . Tính thể tích khối chóp theo công thức 
+ Cách 2 
 . Xác định đa giác đáy 
 Chuyên đề: Khối đa diện và thể tích khối đa diện TRƯỜNG THPT NGUYỄN DU 
 . Tình các tỷ số độ dài của đường cao (nếu cùng đa giác đáy) hoặc diện tích đáy (nếu cùng đường cao) 
của khối chóp “nhỏ” và khối chóp đã cho và kết luận thể tích khối cần tìm bằng k lần thể tích khối đã 
cho 
+ Cách 3: dùng tỷ số thể tích 
Hai khối chóp S.MNK và S.ABC có chung đỉnh S và góc ở đỉnh S S
 V SM SN SK
Ta có : S. MNK .. 
 VS. ABC SA SB SC
 M K
 n
 N
 A
 C
 B
B. MỘT SỐ CÔNG THỨC GIẢI TAM GIÁC VÀ CÔNG THỨC TÍNH DIỆN TÍCH 
1. Hệ thức lượng trong tam giác vuông: Cho tam giác ABC vuông tại A ta có 
 _A 
 - Định lý pitago: BC2 AB 2 AC 2 
 22
 - BA BH.;. BC CA CH CB b 
 c _h 
 BC = 2 1AM 1 1
 - 2 2 2 
 Tỷ số AHlượng giác AB trong AC tam giác vuông : 
 2 c’ b’ 
 - AH BH. CH _C 
 _B _H a M_ 
2. Hệ thức lượng trong tam giác thường: 
* Định lí hàm số côsin : a2 b 2 c 2 2 bc . c osA 
 a b c
* Định lí hàm số sin : 2R ( R : Bán kính đường tròn ngoại tiếp ABC ) 
 sinABC sin sin
3. Các công thức tính diện tích: 
a. Công thức tính diện tích tam giác: 
 1
 - S .. BC AH 
 ABC 2
 1abc . . abc 
 - S . ABAC . .sin A pr . ppapbpc .( ) Với p 
 ABC 24R 2
* Đặc biệt: A
 b
 1 c
 + Diện tích tam giác vuông: S .. AB AC 
 ABC 2
 C
 B a
 + Tam giác cân: A
- Đường cao AH cũng là đường trung tuyến 
- Tính đường cao và diện tích 
AH BH.tan B 
 B H C
 Chuyên đề: Khối đa diện và thể tích khối đa diện TRƯỜNG THPT NGUYỄN DU 
 1
S .. BC AH 
 ABC 2 A
 + Tam giác đều 
 G
 C
- Đường cao của tam giác đều B
 M
 3 3
 h AM AB. ( đường cao h = cạnh x ) 
 2 2
 3
- Diện tích : S (). AB 2 
 ABC 4
b. Hình vuông: S = cạnh x cạnh 
c. Hình chữ nhật: S = dài x rộng 
 1
d. Diện tích hình thoi: S = ( chéo dài x chéo ngắn ) 
 2
e. Diện tích hình thang: S = ( đáy lớn + đáy nhỏ ) x chiều cao 
f. Diện tích hình bình hành: S = đáy x chiều cao 
i. Diện tích hình tròn : S = R2 
C. QUAN HỆ VUÔNG GÓC. 
1. Kiến thức cơ bản thường sử dụng: 
 a b;, a b P 
•  dP 
 d a, d b  
• Nếu dP d vuông góc với mọi đường thẳng nằm trong mặt phẳng (P). 
 dd// ' 
•  dP' 
 dP  
 dQ 
•   QP 
 dP  
 PQ  
•  dQ 
 d P , d   
 PQ  
• PRR    
 QR  
2. Góc giữa đường thẳng và mặt phẳng: 
Cách xác định góc giữa đường thẳng d và mặt phẳng (P): 
Tìm hình chiếu d/ của d lên mặt phẳng (P). Khi đó góc giữa d và (P) là góc giữa d và d/ 
3. Góc giữa hai mặt phẳng 
Cách xác định góc giữa hai mặt phẳng (P) và (Q) 
Xác định hai đường thẳng d và d’ nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến tại một 
điểm. Khi đó góc giữa hai mặt phẳng (P) và (Q) là góc giữa hai đường thẳng d và d’. 
 Chuyên đề: Khối đa diện và thể tích khối đa diện TRƯỜNG THPT NGUYỄN DU 
II. CÁC DẠNG BÀI TẬP, CÁC CÂU HỎI MÔ TẢ 
NHẬN BIẾT 
Câu 1: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: 
 1 1
 A. Bh. B. Bh. C. 3.Bh . D. Bh  
 3 2
Câu 2: Cho hình chóp S. ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài 
đường cao không đổi thì thể tích S. ABC tăng lên bao nhiêu lần? 
 1
 A. 4 . B. 2 . C. 3 . D. . 
 2
Câu 3: Có bao nhiêu loại khối đa diện đều? 
 A. 4 . B. 5. C. 3 . D. 2 . 
Câu 4: Cho khối đa diện đều pq;  , chỉ số p là: 
 A. Số các cạnh của mỗi mặt. B. Số mặt của đa diện. 
 C. Số cạnh của đa diện. D. Số đỉnh của đa diện. 
Câu 5: Cho khối lăng trụ có thể tích bằng 58cm3 và diện tích đáy bằng 16cm2. Chiều cao của lăng trụ là: 
 8 87 8 29
 A. cm.. B. cm.. C. cm.. D. cm.. 
 87 8 29 8
Câu 6: Cho S. ABCD là hình chóp đều. Tính thể tích khối chóp S. ABCD biết AB a , SA a . 
 a3 2 a3 2 a3
 A. a3 B. C. . D. 
 2 6 3
Câu 7: Cho hình chóp S. ABC có SA ABC , đáy ABC là tam giác đều. Tính thể tích khối chóp 
S. ABC biết AB a , SA a. 
 a3 3 a3 3 a3
 A. . B. . C. a3 . D. 
 12 4 3
Câu 8: Cho hình chóp S. ABCD có SA ABCD , đáy ABCD là hình chữ nhật. Tính thể tích S. ABCD 
biết AB a , AD 2 a , SA 3 a . 
 a3
 A. a3 . B. 6a3 . B. 2a3 . D.  
 3
Câu 9: Thể tích khối tam diện vuông O. ABC vuông tại O có OA a, OB OC 2 a là 
 2a3 a3 a3
 A.  B.  C.  D. 2a3 . 
 3 2 6
Câu 10: Cho hình chóp S. ABC có thể tích V . MNP,, lần lượt là trung điểm của SA,, SB SC . Thể tích 
SABC.''' tính theo là: 
 V V V V
 A.  B.  C.  D.  
 6 3 8 4
THÔNG HIỂU 
Câu 1: Cho hình hộp ABCDA'''' B C D có thể tích V. Tính thể tích tứ diện ACB'' D theo V. 
 Chuyên đề: Khối đa diện và thể tích khối đa diện TRƯỜNG THPT NGUYỄN DU 
 V V V V
 A. . B. . C. . D. . 
 6 3 8 4
Câu 2: Cho hình chóp S. ABC . Gọi M là trung điểm cạnh SA và N là điểm trên cạnh SC sao cho 
SN 3 NC . Tính tỉ số k giữa thể tích khối chóp ABMN và thể tích khối chóp SABC . 
 3 3 2 1
 A. k . B. k . C. k . D. k . 
 8 4 5 3
Câu 3: Cho hình chóp S. ABC có SA , SB , SC đôi một vuông góc và SA SB SC a . Gọi B , C 
lần lượt là hình chiếu vuông góc của S trên AB , AC . Tính thể tích hình chóp S. AB C . 
 a3 a3 a3 a3
 A. V . B. V . C. V . D. V . 
 12 24 48 6
Câu 4: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và thể tích bằng a3 .Tính chiều 
cao h của hình chóp đã cho. 
 A. ha .. B. ha 2.. C. ha 3.. D. ha 3.. 
Câu 5: Cho hình chóp tam giác đều cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy một góc 
60 . Tính thể tích V của khối chóp. 
 a3 3 a3 2 a3 3 a3 3
 A. V . B. V . C. V . D. V . 
 4 6 8 24
Câu 6: Một hình chóp tứ giác đều có góc tạo bởi mặt bên và mặt đáy bằng 60 và diện tích xung quanh 
bằng 8a2 . Tính diện tích S của mặt đáy hình chóp. 
 A. Sa 4 2 . B. Sa 432 . C. Sa 2 2 . D. Sa 232 . 
Câu 7: Cho khối lăng trụ ABC., A B C M thuộc cạnh AA sao cho MA 3 MA . Tỉ số thể tích của khối 
lăng trụ ABC. A B C và thể tích khối chóp MABC. bằng. 
 A. 12. B. 18. C. 8 . D. 4 . 
Câu 8: Cho khối lăng trụ tam giác ABC. A B C có thể tích là 36cm3 . Gọi M, N lần lượt là trung điểm 
của AA , BB . Tính thể tích V của khối tứ diện AC MN.. 
 A. 4cm3 . B.V 12cm3 . C.V 9cm3 . D.V 6cm3 . 
Câu 9: Cho lăng trụ ABC. A B C có cạnh bên bằng 2a , đáy ABC là tam giác cân tại 
A; AB 2 a ; BAC 1200 . Hình chiếu vuông góc của A trên mp ABC trùng với trung điểm của cạnh 
BC . Tính thể tích khối chóp A . BB C C ? 
 3
 3 3 4a 3
 A. 4a . B. 2a . C. . D. 3a . 
 3
Câu 10: Cho hình lập phương ABCD.'' A B C D có đường chéo AC ' 3a . Tính thể tích của hình lập 
phương theo a. 
 27 2 3 3 3 3
 A. a . B. a . C. 3 3a . D. 27a . 
 8
VẬN DỤNG 
Câu 1: Cho hình chóp S. ABC có SA ABC , tam giác ABC vuông cân tại B , AC 2 a và SA a. 
Gọi M là trung điểm cạnh SB . Tính thể tích khối chóp S.. AMC 
 a3 a3 a3 a3
 A. . B. . C. . D. . 
 6 3 9 12
 Chuyên đề: Khối đa diện và thể tích khối đa diện TRƯỜNG THPT NGUYỄN DU 
Câu 2: Một hình hộp chữ nhật ABCD. A B C D có ba kích thước là 2cm , 3cm và 6cm . Tính thể 
tích của khối tứ diện ACB. D . 
 A. 8 cm3 . B. 12 cm3 . C. 6 cm3 . D. 4 cm3 . 
Câu 3: Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh 
là các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng a. Hãy tính thể tích 
của khối tám mặt đều đó. 
 a3 a3 a3 a3
 A. B. C. D. 
 4 6 12 8
Câu 4: Cho hình chóp tứ giác S. ABCD có SA ABCD . ABCD là hình thang vuông tại A và B biết 
AB 2 a . AD 33 BC a . Tính thể tích khối chóp S. ABCD theo a biết góc giữa SCD và ABCD 
bằng 600 . 
 A. 26a3 . B. 66a3 . C. 23a3 . D. 63a3 . 
Câu 5: Cho khối lăng trụ đứng ABC.''' A B C có đáy là tam giác ABC vuông tại A; AC a ; ACB 60o . 
Đường thẳng BC ' tạo với mặt phẳng AA'' C C góc 300 . Tính thể tích khối lăng trụ đã cho. 
 a3 3. a3 3.
 A. 2a3 3. B. a3 6. C. D. 
 2 3