Đề thi khảo sát chất lượng cuối năm Toán Lớp 12 (Đợt 2) - Mã đề: 911 - Năm học 2021-2022 - Sở GD&ĐT Nam Định (Có đáp án)

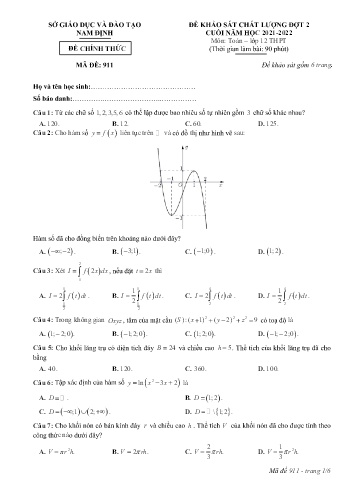
 SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐỢT 2 
 NAM ĐỊNH CUỐI NĂM HỌC 2021-2022 
 Môn: Toán – lớp 12 THPT 
 ĐỀ CHÍNH THỨC (Thời gian làm bài: 90 phút) 
 MÃ ĐỀ: 911 Đề khảo sát gồm 6 trang. 
Họ và tên học sinh: 
Số báo danh: . .. 
Câu 1: Từ các chữ số 1,2,3,5,6 có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số khác nhau? 
 A. 120. B. 12. C. 60. D. 125. 
Câu 2: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ sau: 
Hàm số đã cho đồng biến trên khoảng nào dưới đây? 
 A. ;2 . B. 3;1 . C. 1;0 . D. 1;2 . 
 2
Câu 3: Xét I f 2 x dx , nếu đặt tx 2 thì 
 1
 1 1 1 4 1 4
 A. I 2 f t dt . B. I f t dt . C. I 2 f t dt . D. I f t dt . 
 1 2 1 2 2 2
 2 2
Câu 4: Trong không gian Oxyz , tâm của mặt cầu (S ):( x 1)2 ( y 2) 2 z 2 9 có toạ độ là 
 A. 1; 2;0 . B. 1;2;0 . C. 1;2;0 . D. 1; 2;0 . 
Câu 5: Cho khối lăng trụ có diện tích đáy B 24 và chiều cao h 5. Thể tích của khối lăng trụ đã cho 
bằng 
 A. 40. B. 120. C. 360. D. 100. 
Câu 6: Tập xác định của hàm số y ln x2 3 x 2 là 
 A. D . B. D 1;2 . 
 C. D ;1  2; . D. D \ 1;2. 
Câu 7: Cho khối nón có bán kính đáy r và chiều cao h . Thể tích V của khối nón đã cho được tính theo 
công thức nào dưới đây? 
 2 1
 A. V r2 h. B. V 2. rh C. V rh. D. V r2 h. 
 3 3
 Mã đề 911 - trang 1/6 Câu 8: Số phức liên hợp của số phức zi 23 là 
 23 23
 A. i . B. 23i . C. i . D. 23 i . 
 13 13 13 13
Câu 9: Tìm sin5xdx . 
 cos5x cos5x
 A. C . B. C . C. 5cos5xC. D. cos5xC. 
 5 5
 32x 
Câu 10: Phương trình đường tiệm cận ngang của đồ thị hàm số y là 
 21x 
 3 2 1
 A. y . B. y 2. C. y . D. y . 
 2 3 2
Câu 11: Tập nghiệm của phương trình 2log2 xx 3log 1 0 là 
 11 11
 A. 10;10. B. ; . C. 10;100 . D. ; . 
 10 10 10 100
Câu 12: Trong mặt phẳng toạ độ Oxy , điểm biểu diễn số phức zi 3 là 
 A. P 3;1 . B. Q 3; 1 . C. M 3;1 . D. N 1; 3 . 
Câu 13: Cho hàm số ye x , khẳng định nào dưới đây đúng? 
 ex 1
 A. y'. x ex 1 . B. y ' . C. ye' x 1 . D. ye' x . 
 x 1
 x 2
Câu 14: Đồ thị hàm số y đi qua điểm nào trong các điểm dưới đây? 
 21x 
 4
 A. N 2; . B. P 1;1 . C. Q 0; 2 . D. M 1; 3 . 
 3
Câu 15: Phần ảo của số phức z 1 2 i 3 i là 
 A. 5. B. 2. C. 3. D. 1. 
Câu 16: Cho các hàm số y f x ; y g x liên tục trên ab;  . Diện tích S của hình phẳng giới hạn 
bởi đồ thị các hàm số và các đường thẳng x a; x b được tính bởi công thức 
 bb bb
 A. S f x dx g Oxyz x dx . B. S f x dx g x dx . 
 aa aa
 b b
 C. S f x g x dx . D. S f x g x dx . 
 a a
Câu 17: Hàm số y 2 x42 3 x 3 có mấy điểm cực trị? 
 A. 1. B. 2. C. 4. D. 3. 
Câu 18: Trong không gian , mặt phẳng (P ): 2 x 4 y 5 z 5 0 đi qua điểm nào dưới đây? 
 A. M 0;0;1 . B. N 2;1;1 . C. P 2; 1; 1 . D. Q 2;1; 1 . 
Câu 19: Giá trị nhỏ nhất của hàm số y x3 3 x trên  2;0 là 
 A. 2. B. 1. C. 2. D. 0. 
Câu 20: Diện tích S của mặt cầu bán kính r được tính theo công thức nào dưới đây? 
 4 4
 A. Sr 2. B. Sr 2. C. Sr 4. 2 D. Sr 3. 
 3 3
 Mã đề 911 - trang 2/6 Câu 21: Số giao điểm của đồ thị hai hàm số y 2 x32 3 x 1 và y x2 31 x là 
 A. 1. B. 2. C. 3. D. 0. 
Câu 22: Giá trị nhỏ nhất của hàm số y x. ex trên ;0 bằng 
 1 1 1
 A. . B. . C. . D. 0. 
 e e e2
Câu 23: Cho a là số thực dương, biểu thức 3 a viết dưới dạng luỹ thừa với số mũ hữu tỉ là 
 3 1 5 2
 A. a 2 . B. a 6 . C. a 6 . D. a 3 . 
 xt 1
Câu 24: Trong không gian Oxyz , đường thẳng d:2 y t có một vectơ chỉ phương là 
 zt 12 
 A. u1 1; 1;2 . B. u2 1;2; 1 . C. u3 1;1; 2 . D. u4 1;1;2 . 
Câu 25: Cho khối chóp có diện tích đáy B và chiều cao h . Thể tích V của khối chóp đã cho được tính 
theo công thức nào dưới đây? 
 1 4
 A. V Bh. B. V Bh. C. V 6. Bh D. V Bh. 
 3 3
 1
Câu 26: Tìm công bội q của cấp số nhân u biết u , u 2 . 
 n 1 4 4
 1 1
 A. q 2 . B. q 2 . C. q . D. q . 
 2 2
Câu 27: Trong không gian , cho hai vectơ u (1; 3; 2) và v ( 2;1; 1) . Tọa độ của vectơ uv 
là 
 A. ( 3;4;1). B. (3; 4; 1). C. (1;2;3). D. ( 1; 2; 3). 
Câu 28: Cho hàm số y f x có bảng biến thiên như hình vẽ sau: 
 Oxyz
Số nghiệm của phương trình 2fx 5 0 là 
 A. 4. B. 1. C. 3. D. 2. 
 0 x 1
Câu 29: Tính I dx . 
 1 x 1
 A. I 1 2ln 2 . B. I 1 2ln 2. C. I ln 2 1. D. I 2ln 2 1. 
Câu 30: Một chiếc hộp đựng 7 viên bi màu trắng, 6 viên bi màu xanh, 5 viên bi màu vàng và 4 viên bi 
màu đỏ. Lấy ngẫu nhiên 4 viên bi trong hộp. Tính xác suất để trong 4 viên bi được lấy có ít nhất 2 viên bi 
cùng màu. 
 185 230 1 152
 A. . B. . C. . D. . 
 209 307 16 285
 Mã đề 911 - trang 3/6 Câu 31: Tìm z biết 1 2i z 3 4 i 2 z 3 . 
 12 9 13 7 17 14 14
 A. zi . B. zi . C. zi . D. zi . 
 55 55 55 55
Câu 32: Gọi H là hình phẳng giới hạn bởi các đường y x x2 ;0 y . Tính thể tích khối tròn xoay 
được tạo thành khi quay quanh trục Ox . 
 3 2 5 
 A. . B. . C. . D. . 
 4 6 3 6
Câu 33: Hàm số nào dưới đây có đồ thị như đường cong trong hình bên? 
 3
 A. y x32 x 1. 
 2
 13
 B. y x32 x 2 . 
 32
 13
 C. y x32 x 2. 
 32
 D. y x32 32 x . 
Câu 34: Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 1. Khoảng cách từ C đến mặt phẳng 
 SBD bằng 
 2
 A. 1. B. 2. C. 2. D. . 
 2
 x y 23 z
Câu 35: Trong không gian Oxyz , cho điểm M(2; 1;0) và đường thẳng d : . Mặt phẳng 
 2 4 5
đi qua M và vuông góc với d có phương trình là 
 A. 2x 4 y 5 z 8 0. B. 2x 4 y 5 z 0. 
 C. 2x 4 y 5 z 8 0. D. 2xy 0. 
Câu 36: Trong không gian Oxyz, cho hai điểm AB 2; 3; 1 , 4;5; 3 và mặt phẳng 
 P : x y 3z 10 0. Đường thẳng d đi qua trung điểm của AB và vuông góc với mặt phẳng P có 
phương trình là 
 x 3 y 1 z 2 x 3 y 1 z 2
 A. . B. . 
 1 1 3 1 1 3
 x 1 y 1 z 3 x 1 y 4 z 1
 C. . D. . 
 3 1 2 1 1 3
 1
Câu 37: Tập nghiệm của bất phương trình 2x 3 là 
 4
 A. 5; . B. 1; . C. ;5 . D. ;1 . 
Câu 38: Cho hình lập phương ABCD. A B C D . Góc giữa hai đường thẳng BA và CD bằng 
 A. 60 . B. 45 . C. 30 . D. 90 . 
 Mã đề 911 - trang 4/6 5x
Câu 39: Cho hàm số fx . Gọi ab, là các số thực dương thoả mãn 
 55x 
 44 2 22 16
 f a b 31 ab f 1. Tìm giá trị lớn nhất của biểu thức P a b 22 . 
 ab ab 2
 8 20 16 25
 A. . B. . C. . D. . 
 3 3 3 3
Câu 40: Cho hàm số fx xác định trên 0; , có đạo hàm đến cấp hai thỏa mãn 
 1
 f x ln x ,x 0; . Biết f ' 1 0 ; f 1 , tính f 2 . 
 4
 A. f 2 2ln 2 1. B. f 2 3ln 2 2. C. f 2 ln 2 1. D. f 2 ln 2 2. 
Câu 41: Cho hàm số y f() x có bảng biến thiên như hình vẽ sau: 
 éù1 2
Đặt g( x)=- fêú( f( x)) f( x) . Phương trình gx'0 có bao nhiêu nghiệm phân biệt? 
 ëûêú2
 A. 8. B. 7. C. 9. D. 6. 
Câu 42: Cho hàm số f x ax4 bx 3 cx 2 dx e , a 0 và g x mx32 nx px q . Đồ thị các hàm 
số fx và gx cắt nhau tại 3 điểm có hoành độ lần lượt là 3; 1 và 1. Biết fg 00 , tính 
3
2 f x g x 
 dx . 
1 f x g x 
2
 37 49 23 63
 A. ln . B. ln . C. ln . D. ln . 
 62 87 51 95
Câu 43: Cho một khối trụ có bán kính đáy bằng r. Gọi O và O ' lần lượt là tâm của hai đáy. Mặt phẳng 
 P song song với OO và chia khối trụ thành hai phần. Gọi V1 là thể tích phần khối trụ chứa OO , V2 là 
 V r 2
thể tích phần còn lại của khối trụ. Tính tỉ số 1 , biết rằng cách một khoảng bằng . 
 V2 2
 23 3 25 32 
 A. . B. . C. . D. . 
 2 2 2 2
Câu 44: Có bao nhiêu giá trị thực của tham số m để phương trình z22 2 m 1 z m 3 0 có hai 
nghiệm zz12, thoả mãn z1 z 2 z 1 z 2 ? 
 A. 4. B. 1. C. 2. D. 3. 
 2
Câu 45: Gọi zz12, là các số phức thoả mãn z1 1, iz2 1 3 i 2 . Khi z1 z 1 z 2 1 đạt giá trị lớn nhất 
thì z12 z 21 i bằng 
 A. 3. B. 22. C. 1. D. 2 . 
 Mã đề 911 - trang 5/6 Câu 46: Cho hình chóp S. ABCD có đáy là hình thang ABCD vuông tại A và D ; AB 22 AD CD ; 
 a 42
SA vuông góc với đáy; góc giữa SC và đáy bằng 60. Biết khoảng cách từ B đến SCD bằng , 
 7
tính thể tích của khối chóp S. ACD. 
 6 6 6 36
 A. a3. B. a3. C. a3. D. a3. 
 3 2 6 2
 x 12 y z
Câu 47: Trong không gian Oxyz , cho đường thẳng d :, mặt phẳng 
 1 2 1
(P ): x y 2 z 5 0 và điểm A(1; 1;2). Đường thẳng đi qua A cắt đường thẳng d và mặt phẳng 
 uuur uuur
(P) lần lượt tại MN, sao cho AM= 2, AN biết rằng có một vectơ chỉ phương u a; b ; 1 . Khi đó 
ab bằng 
 A. 4. B. 2. C. 5. D. 4. 
Câu 48: Trong không gian , cho mặt cầu (S): x2 +( y - 1)22 +( z + 5) = 36 và bốn điểm 
ABCD(1;2;0) ,( 3;-- 1;2) ,( 1;2;2) ,( 3; 1;1) . Gọi M( a;; b c) là điểm nằm trên mặt cầu (S) sao cho biểu 
thức T= MA2 +24 MB 2 - MC 2 - MD đạt giá trị nhỏ nhất. Tính abc++. 
 22 22 34
 A. . B. 2. C. . D. . 
 7 7 7
 2x 4 1
Câu 49: Có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình 0? 
 log1 x 4 4
 2
 A. 10. B. 8. C. 9. D. 11. 
Câu 50: Cho hàm số f( x ) ax4 bx 3 cx 2 dx e , a 0 có đồ thị như hình vẽ. 
Có bao nhiêu giá trị nguyên của tham số m  10;10 để hàm số g x f22 x mf x 43 m có 
đúng 5 điểm cực trị? 
 A. 14. B. 13. C. 15. D. 16. 
 ---------- HẾT ---------- 
 Mã đề 911 - trang 6/6