Ôn tập môn Toán học Lớp 9 - Bài 1: Căn bậc hai

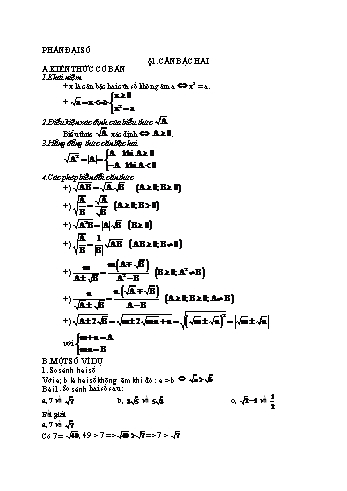
ủa các biểu thức sau:
a, Có nghĩa khi 
Vậy có nghĩa khi 
b, Có nghĩa khi 
c, Có nghĩa khi 
d, Có nghĩa khi 
e, Có nghĩa khi 
f, có nghĩa khi 
Bài 5. Tìm điều kiện có nghĩa của các biểu thức sau:
a, có nghĩa khi 	
b, 	Có nghĩa khi 
c, Có nghĩa khi 
3. Rút gọn và tính giá trị của biểu thức
Bài 6. Cho a = b = 
Tính a + b; a – b; a.b; a:b
Bài 7. Rút gọn
e, E = =
f, F = = 
	= 
g, G = = 
h, H = =
Bài 8.Cho biểu thức 
	a) Rút gọn y. Tìm x để y = 2.
	b) Cho x > 1. Chứng minh 
	c)Tìm giá trị nhỏ nhất của y
Giải
a,
	(Ở đây ta có thể áp dụng giải phương trình bậc hai bằng cách đặt ẩn phụ)
	b) Có 
c) Có: 
	Vậy 
Bài 9. Cho biểu thức A = 
a, Rút gọn biểu thức A.
A= = 
+ Với thì A = 
+ Với thì A = 
b, Tính giá trị của A biết x = = 
Có nên A = -1
Bài 10. Cho biểu thức M = 
a, Tìm điều kiện xác định của M.
b, Rút gọn biểu thức M.
M = = 
 = 
c, Tính giá trị của biểu thức M biết a = = 
Khi ấy M = 	
4. Chứng minh đẳng thức
A = B ó 
Bài 11. Chứng minh đẳng thức sau:
a, 	b, 
c, 	d, 
Bài 12. Chứng minh đẳng thức sau:
Bài giả
a, = 
 = = 2.4 = 8 =VP
Vậy đẳng thức được chướng minh
b,= 
Bài 13. Chứng minh đẳng thức sau:
	 với điều kiện đã xác định
 Bài 14. Chứng minh đẳng thức sau:
Bài giải
a, Đẳng thức đã cho tương đương 
 luôn đúng
Vậy đẳng thức được chứng minh
b, VT= 
 = = 
 = = = VP
Vậy đẳng thức được chứng minh
5. Phương trình có căn thức
Bài 15. Giải phương trình sau:
a, ĐK:
thỏa mãn ĐK
Vậy phương trình có nghiệm x=5
b, 
x – 1 = 5
x – 1 = -5
Vậy phương trình có nghiệm x = 6; x = -4	
c,. ĐK: 
Có x = -7 không thỏa mãn ĐK
Vậy phương trình có nghiệm x = -1
Bài 16. Giải phương trình sau:
a, ĐK 
	 (thỏa mãn đk)
Vậy phương trình có nghiệm 
b, ĐK: 
(thỏa mẫn điều kiện)
c, 	ĐK:x > 3
Có x = 3 không thỏa mãn ĐK
Vậy phương trình có nghiệm x =5
d, ĐK 
Đặt 
Khi ấy 
C.MỘT SỐ BÀI TẬP CƠ BẢN
Bài 1.Thực hiện phép tính, rút gọn biểu thức
	a, 
	b. 
	c. 
	d. 
	e. 
	f. 
	g. 
	i. 
	k. 
	g. 
	j. 
Bài 2...ại x bằng giá trị biểu thức A.
Bài 13 Cho biểu thức: P = ()
	a) Rút gọn biểu thức P.
	b) Tìm các giá trị của x để P <1
Bài 14
1. Rút gọn biểu thức: A = .
2. Cho biểu thức () .
 	 	a) Rút biểu thức B
 	b) Tìm tất cả các giá trị của x để .
Bài 15 
Tính giá trị của biểu thức 
Cho biểu thức: (với )
	a. Rút gọn biểu thức K.
	b. Tìm a để .
Bài 16
1, Tính A = 
2, Cho biểu thức ( Điều kiện và ) 
 a, Rút gọn biểu thức P
b, Tìm giá trị của x để P > 0.
Bài 17
1. Tính giá trị biểu thức : A = 
2. Cho biểu thức : B = với x 0, x 9
a. Rút gọn B
b. Tìm x để B > 2
Bài 18. Cho hai biểu thức A = 
 và B = (với x0, x1)
a) Rút gọn biểu thức A và B
b) Với giá trị nguyên nào của x thì giá trị của biểu thức B lớn hơn giá trị của biểu thức A?
 Bài 18
 1. Rút gọn biểu thức
A = 
 2. Cho biểu thức B = , với 0 ≤ x ≠ 1
a) Rút gọn B
b) Tính giá trị biểu thức B khi x = 
Bài 20. Cho hai biểu thức và với .
Tính giá trị của biểu thức A khi x = 9
Chứng minh 
Tìm tất cả các giá trị của x để .
Bài 21
1.1. Rút gọn biểu thức sau: 
1.2. Cho biểu thức: 
Với 
a. Rút gọn M
b. Tính M khi 
c. Tìm a đề 
Bài 22 Cho các biểu thức:
 B = với .
a) Rút gọn các biểu thức A, B. 
b) Tìm các giá trị của x để .
Bài:23 
1. Tính 
2. Cho biểu thức 
Rút gọn biểu thức P
Tìm giá trị của x để P > 0.
Bài 24 Cho biểu thức P = với x > 0 và x ¹ 1
 1.1. Rút gọn P	
 1.2. Tìm giá trị của x biết P = 3
Bài 25. Cho hai biểu thức và (Đk: )
a) Rút gọn biểu thức A, B. 
b) Tìm các giá trị của x để giá trị biểu thức A bằng giá trị biểu thức B.
Bài 26. 1. Cho biết a = và b = . 
Tính giá trị biểu thức: P = a + b – ab.
 	 2. Cho biểu thức B = , với 0 ≤ x ≠ 1
a) Rút gọn B
b) Tìm x để .
Bài 27. 
 1. Rút gọn biểu thức: 
 2. Cho biểu thức với 
a) Rút gọn biểu thức B
b) Tìm a để B < 0 
Bài 28. Cho biểu thức A = .
1.1) Nêu điều kiện xác định và rút gọn biểu thức A.
1.2) Tìm x để A < 1.
Bài 29.
1, Tính 
2, Cho biểu thức ( Điều kiện và ) 
 a, Rút ...i a1 ≠ a2.
	+Nếu b1 = b2 thì chúng cắt nhau tại b1 trên trục tung.
	+Nếu a1.a2 = -1 thì chúng vuông góc với nhau.
Ví dụ 1: Cho hàm số y = 2x + m2 – 3 và hàm số bậc nhất y = (m + 1)x + 4
a, tìm m để hai đồ thị hàm sổ trên cắt nhau? Hai đồ thị hàm số trên có song song không
b, tìm m để hai đồ thị hàm số trên đi qua điểm A(1;3)
Ví dụ 2: Cho hàm số bậc nhất y = (m – 2)x +2m – 1 có đồ thị (d). Tìm giá trị của m biết:
a, (d) đi qua A(2;3)
b, (d) cắt trục hoành có hoành độ bằng 3;
c, (d) Cắt đường thẳng y = -2x – 1 tại điểm có hoành độ bằng -3;
d; (d) cắt đường thẳng y = 2x-3 tại điểm cách trục hoành một khoảng bằng 2.
2.Hệ phương trình bậc nhất
	Cách giải chủ yếu dựa vào hai phương pháp cộng đại số và thế. Chú ý phương pháp đặt ẩn phụ trong một số trường hợp xuất hiện các biểu thức giống nhau ở cả hai phương trình.
B. BÀI TẬP VẬN DỤNG
Bài 1.
 a) Tìm m để đường thẳng y = 2x - 3 và đường thẳng y = (m - 1)x + m - 2 cắt nhau tại một điểm trên trục tung.
 b) Giải hệ phương trình sau: 
Bài 2.
1. Cho đường thẳng (d): y = ( m – 2 )x + m và (d’): y = 2x + 7- m .Với giá trị nào của m thì đường thẳng (d) cắt đường thẳng(d’) tại một điểm trên trục tung.
2. Giải hệ phương trình : 
Bài 3
1) Cho đường thẳng (d): y = 2x + 1. Với giá trị nào của m thì đường thẳng (d) cắt đường thẳng y = (m - 2 )x + m tại một điểm trên trục tung.
2) Cho hệ phương trình (m là tham số) 
a) Giải hệ phương trình khi m = 3
b) Tìm m để hệ phương trình có nghiệm duy nhất (x, y) thỏa mãn x2 + y2 đạt giá trị nhỏ nhất.
Bài 4.
1. Xác định hàm số y = ax + b biết đồ thị của hàm số song song với đường thẳng y = –2x – 3 và cắt trục tung tại điểm có tung độ bằng 2018
2. Giải hệ phương trình 
Bài 5.
a) Cho hàm số (d). Tìm giá trị của a và b để đường thẳng (d) cắt trục tung tại điểm có tung độ và cắt trục hoành tại điểm có hoành độ bằng -1.
b) Cho hệ phương trình: (1)
Tìm m để hệ (1) có nghiệm duy nhất (x; y) thỏa mãn: .
1) Tìm giá trị của m để đồ thị của các hàm số y = x + (2 + m) và y = 2